ゼルコバの木テント村

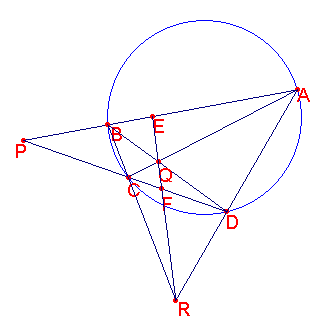
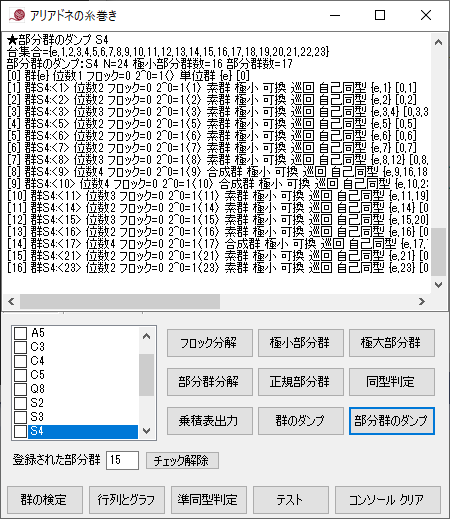
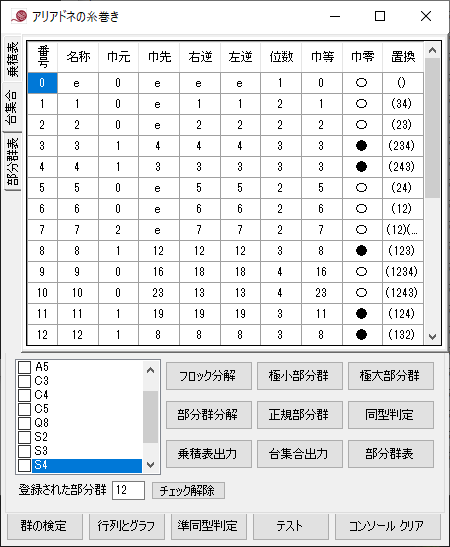
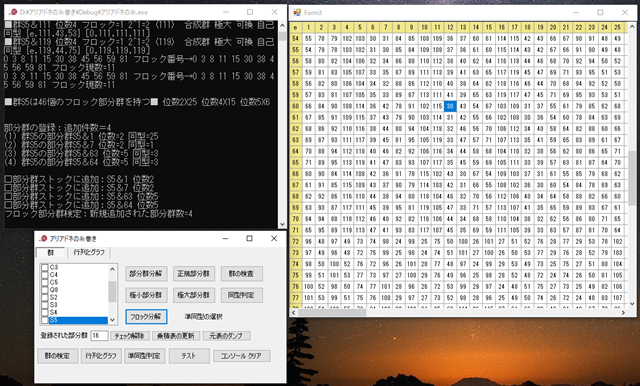
円 Γ と Γ 上にない点 P が与えられている．P を通る円と交わる２直線を引き，円との交点をそれぞれ A, B および C, D， ２直線 AC, BD の交点を Q,２直線 AD, BC の交点を R とする．このとき，直線 QR は直線 PAB, PCD の取り方によらず定まり，この直線 QR を点 P の円 Γ に関する極線という．

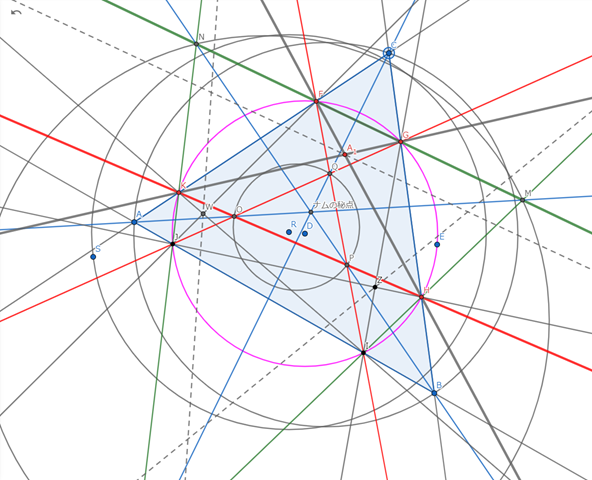
ナムのマル秘点の作図例で言えば，上図の点Pは三角形ABCの頂点Aに該当し，円Γは⊿ABCと交接する円であるから，円との交点A, B, C, D はF, KとJ, I に相当すると考えられるが，作図例にはAC, BD，およびAD, BCに相当する直線，すなわち，FJ, KI と FI, KJ のうち，KI は作図されていないため，交点Qは図面上には現れない．また，FIとKJの交点は２直線が平行に近い位置にあるため図面外に出てしまっている．⇒すべての交点が見えるようにアレンジしてみた．図面が混み合ってしまうが，上のモデルに従って直線を追加してみよう．

上図の点線が点Aと円Γのよって定まる「極線」と考えられる．しかし，今のところ，この線とナムの三角図にはどのような関係も見出し得ない．他の２頂点も同様の極線を持っているはずなので，追加してみることにしよう．頂点Bの場合は，I, H, G, JがA, B, C, Dに相当するのでこれらを結ぶ直線を追加してみる．⇒一応，頂点A, B, Cに対応する３本の極線を引くことができた．

確かに，これらが１つの点と円の関係によって定まることは明らかだ．頂点A, B, Cを移動すると，それらに関係する極線のみ変化し，他の２頂点に関するものは不動の位置に留まる．また円を移動すると３本の極線が同時に変化するので，点と円によって一意に定まっているということは明らかだ．ただし，よく見るとこれはそれほど不思議でも何でもない．円外の１点を通る２本の接線の接点を結べば，単純にこれらの極線が現れる．もちろん，ナムの三角図と無関係ではあり得ないとしても，ただちに何か言えるような直接的つながりは今のところ見当たらない．

円の中心O以外の任意の点を極とする極線が存在すると言っているのと実質的にはまったく同じことだ．従って，この極線を求めることは今の事例ではほとんど意味がないと考えられる．というか，この記事の筆者はそこから，「極線の別定義」を引き出しているので，無意味と言っては失礼になるかもしれない．⇒ここから，相反変換というのが導出され，それを使ってパスカルの定理を証明するというところまで進む．

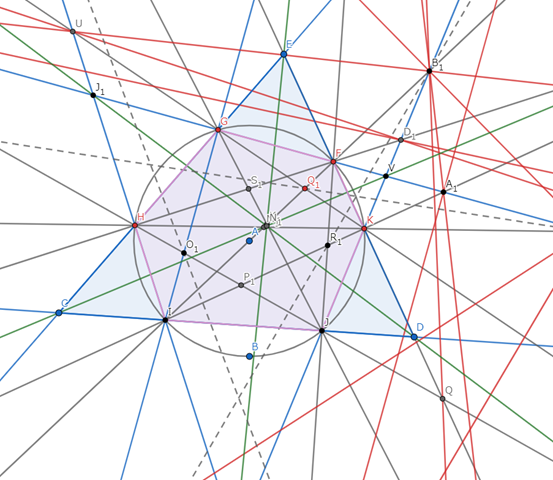
パスカルの神秘六芒星図にはすべての交点と交線が書き込まれているかどうか確認しておこう．⇒少なくとも６点を結ぶ直線はすべて記入されている．それらの交点が確定しているかどうか確認する必要がある．直線は１５本で，６角形の辺を除くと９本だから，１本の直線は８個の交点を持たなくてはならない．９本の直線をすべて確認した訳ではないが，一応８交点を持つということにはなっているようだ．

いや，交点のすべては描画されていない．また，これら交点を結ぶ直線，つまり極線は描かれていない．円の内部の交点が見落とされているようだ．⇒一応，「極線」を描画（点線）してみたが，パスカル線とはあまり縁がないような感じだ．

これらの極線はすべて円より内側に描画されている．

テント村の会社住所が間違っているのに気付いた．1-3-72が1-7-32になっていた．同じ内容で２箇所修正する必要があった．ずっと触っていないのでどこを直せばよいのか見当も付かない状態だったが，あきらめる訳にもゆかないので，なんとか粘って修正した．夕方になって来訪者カウントが１７万を超えた．

１５万から１７万までかなり早かったような気がする．次の目標は２０万突破だ．１年で目標達成できるだろうか？それにしても，来訪者カウントは日によってかなりむらがある．理由はよく分からない．

今日は買い物を予定しているので，昨日は早めに休んで早起きしようとしたのだが，午前１時を回ったところで目が覚めて起きてしまった．これでは却って時間調整が難しくなる．仕方ないので少し仕事してからもう一度寝ることにしたが，テント村の来訪者カウントがまだ午前１時台というのに９００を超えている．これはどういうことなのだろう？

午前４時で922．大して進んでいないが，まだ日は長いので今日中に１７万アクセスを超えるのではないだろうか？⇒いや，届かなかった．いま午後11時少し前，Visitors Today は 1000を超えたものの，カウントは169569 でまだ大分先がある．午前０時から２時までの間で900を超えていた理由は分からない．時計が壊れていたのではないとは思うが…

どうも，ちょっと様子がおかしい．今朝起きたら，このマシンが落ちてロック画面になっていた．ログインして入ったがいくつか不審な点がある．Libere Draw を開こうとして，間違えてmaxima が開いた．なぜ間違えたかというと，アイコンの並びが変わっていたためだ．Libre Draw ほか，いくつかのアイコンがタスクバーから消えている．maxima は立ち上がって来たが「コマンドが実行できない」という．

この後に以下のパネルが続く．

OKを押してアプリは一応立ち上がった．Libre Draw はメニューから立ち上げることができた．Libre Math も起動できた．クロームは開いていて，新機能の紹介ページが一面になっていたので，この一連の不具合はおそらくクロームの自動更新によるものだろう．

https://www.geogebra.org/m/etvryqed

使い方はまだよく分からないが，最強のツールであることは明らかだ．ICAROSでやりたかったこと，あるいはそれ以上のことが実現されていると言ってもよい．GeoGebraはラテンアメリカ系のサイト※だが，Googleと繋がっているのだろうか？Googleクラスルームに割り当てるということができるようだ．※これは間違い．

GeoGraphはBYJU’Sというインドの教育機関と繋がっている．GeoGebraは南米系と思い込んでいたが，本社はオーストリアのリンツにあり，Markus Hohenwarterという人物が経営している．BYJU’Sと繋がっているというより，買収されたと見た方がよいかもしれない．BYJU’Sというのは元々は数学の教師集団だったようなのだが… 一応NPOという位置付けでよいようだ．BYJU’Sは多分ネットワーク通信教育が本業と思われるが，かなりの資金は中国から流入している模様だ．

GeoGraphのページはHTMLに埋め込むことができるので，「テスト投稿」としてアップロードしてみた．昨日見たときは真っ白で何も表示されていなかったのだが，今日は図面が表示されていて，ドラッグなどの操作もできるようになっている．あるいは，画面の余白部分しか見えていなかったためかもしれない．一つ面倒なことがある．このページを離れようとすると，以下のパネルが出てくることだ．

保存できれば，保存して移りたいのだが，どこにもそれらしきコマンドは見当たらない．これは一般公開されている記事だが，おそらく「共有」としているためだろう．GeoGraphの公開されているページはほとんど編集権を所有者に限定しているみたいなので，「共有」設定にしていること自体がイレギュラーなのだろう．

GeoGebraにはオフラインで使えるアプリがいくつかある．

1. GeoGebraスィート
2. 関数グラフ
3. 空間図形
4. 幾何
5. 数式処理（CAS）
6. 全機能統合版・クラシック６
7. 全機能統合版・クラシック５

多分項１のスィートというのは，「全機能統合版」の最新版ということではないかと思う．とりあえず，これをインストールしてみよう．⇒これを使うのは「作業」になってしまうと思われるので，開発機にインストールした方がよいかもしれない．開発機にはメモリ16GBが搭載されているが，こちらには４GBしか載っていない．ディスクも開発機には京単位の外付けが繋がっている．

開発機にスィートをインストールした．これでローカルでもGeoGraphが使えるようになったが，いま，ネット上にあるデータをアプリに移すにはどうしたらよいのだろう？いや，それはすでにやっている．SDCにGeoGebraというフォルダを作ってそこに落としてある．

ナムの三角形作図 by GeoGebra

台集合の属性リストをマトリックス表示できるようになった．もう少し手を入れるところはあるが，先に部分群表を出すところを片付けてしまおう．部分群表というのは現在部分群のダンプとしているところをマトリックスに整形表示するというものだ．

▲S4<3,7>を選択してフロック分解で配列の範囲外の例外が発生した．例外はフロック現数のカウントで起きている．フロック部分群検定ではD集合という配列を管理している．対象となる部分群の位数は12でフロック配列はこのサイズで作られているが，元表[9].フロック番号には16という値が入っているため，障害が発生する．

S4<3,7>は部分群検定で生成・登録された部分群だが，元表などを初期化していないのではないだろうか？フロック番号は最初のフロック分解で設定されているはずだが…⇒部分群を新規生成する場合には，元表を渡さないようにした．ただし，これでも不一致は発生する．追加登録で事後にノードを追加しているためだ．部分群の追加というところで元表を再計算することにする．

▲S4の部分群表を表示した後，台集合出力しようとして置換積に変換で停止した．引数のarrayが空で呼び出されている．元属性表の作成を実行しているところで，置換構成は空ではないため元g.置換を置換積に変換しようとしているのだが…単位元に置換が設定されていないのではないか？⇒かなりよい動きになってきた．

部分群表で同型の部分群の個数を表示するようにしたい．部分群の追加のところでこの値は算出されているので，どこかに保存しておけばよい．また，台集合のリストは{}で囲む必要はない．DataGridViewでは，末尾の一行は行追加のために予約されているようで，カラムを指定してソートしても，最後の行が残ってしまう．テーブルのサイズを１大きくして余分な行を表示するようにしたらまともな動作になった．

▲群表では番号は１発進になっている．元表でも同様にした方がよいのではないか？ただの表示なので特に問題ないはずだ．もともと元.番号に0が入っているのが問題なのではないか？ただし，単位元はフロック〇と呼んでいるようにすでに番号〇として認識されているかもしれない．単位元の現番号は〇でよいのではないだろうか？冪零などという話も出てくるので… とりあえず，現状のままとしておこう．

乗積表出力で以下のエラーになった．

多分，フォームを閉じてしまったのだと思う．Form3のFormClosingでイベントをキャンセルして，隠蔽するようにした．乗積表出力を再度押せば，元の位置に開かれる．本体画面の上半分にテキストボックス表示して，久留島喜内の道具箱のような作りにしてみた．①群のダンプと②部分群のダンプが表示される．

これだけでも十分役に立つと思われるが，これを乗積表のようにマトリックス表示してみたい．多分ずっと見易くなると思われるが，マトリックス表示する最大の利点は列でソートできるという点だ．これができると一つの情報を色々な角度から分析できるのでとても有用だと思う．ただし，元表と部分群表を出すとすれば，乗積表だけ別画面というのもおかしいので，また元に戻すということになるだけでなく，少なくとも３種のテーブルを切り替えて同時に開くことができなくてはならないだろう．そのためにはタブが必要になってくる．一応タブの準備はできた．ともかく台集合を出してみよう．⇒乗積表を主画面に戻した．