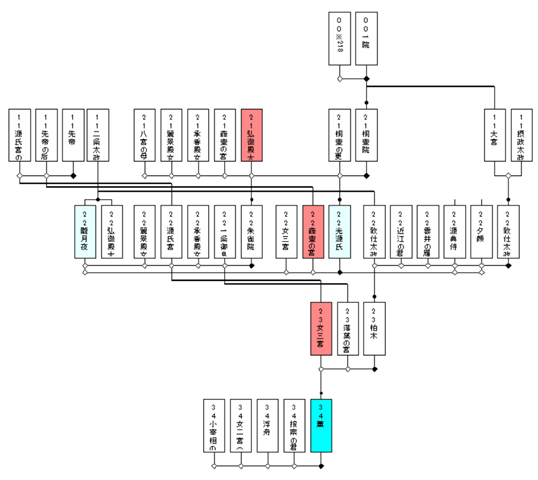
これまで「重婚同類」と呼んできた「婚姻関係で連結したカード集合」を「重婚クラスタ」と呼んでみることにした.「セックスつながりのグループ」を俗になんと言っているのか分からないが,「重婚クラスタ」とはまさにそのような関係で連結したグループ以外のなにものでもない.薫のZ木家系図の登場人物は全36名だが,そのうち最大の重婚クラスタには23名ものメンバーが加わっている!重婚クラスタは「同値類」なので,あるクラスタに属するメンバーは他のクラスタとはまったく関わりがない.つまり,クリスプなクラスタである.※
※疫学的なクラスタの定義からはやや離れるが,「コロナ感染者」というグループを一つのクラスタであると考えると,世界中のコロナ感染者は明らかに世界でたった一つのクラスタに属している.コロナ前・コロナ後の世界が変わるというのはこのこと,つまり「世界は一つという事象の顕在化」を意味していると考えられる.
系図図面の縦軸は時間(世代)であり,婚姻関係とはある特殊な時間を共有することであると考えられるので,婚姻関係にあるカードは同世代に属するというのが系図作図上の基本原則である.しかし,世の中には世代差のあるカップルはいくらでも存在する.このようなケースでもその世代差を補助的な垂線(長い尻尾)で補うことによって(2つのカードを同世代に配置することにより)作図可能である.重婚クラスタを節点とし,親子関係を枝とするグラフ(重婚グラフ)を連結成分に分解すると,系図上で多重カードが発生するメカニズムが見えてくる.
重婚クラスタが親子関係によって多段に連結されていたとしても,それだけでは多重カードは発生しない.このような場合にはクラスタを階層的に配置することが可能であり,(同一クラスタに属する)同世代カードはBTWなどの技法によって(連結線を用いることで)単一のカードとして描画できる.多重カード発生の根本原因はこの階層化が循環によって不可能になることにある.(階層=木は閉路を含まない連結グラフである)従って,多重が発生するためには重婚グラフの連結成分が強連結であるか,ないし強連結成分を含むことが必要かつ十分な条件となる.
この条件には一つの重婚クラスタの内部に「親と子」が存在してグラフ的には自己ループを構成する場合を含んでいる.「重婚クラスタ」と言っても,その参加者がすべて「重婚者」であると言う訳ではない.たとえば,薫のZ木家系図のクラスタ23には単婚者が11人も含まれているが,そのうちの一人弘徽殿大后のカードは多重になっている.
重婚グラフは重婚クラスタをノードとし,親子関係を枝とするグラフだが,多重カードの最大の原因が重婚クラスタの内部親子関係であることは事例から明らかだ.ただし,現状では多重枝を登録しようとすると,「多重枝の登録は不可」が表示されて弾かれてしまうので,クラスタ23に関わる自己ループ枝は1つしか登録することができない.このために,重婚クラスタ循環=1ということになっているのだが,これは実態を反映していない.⇒重婚グラフの属性をMULTIEDGEGRAPH(多重枝グラフ)に設定して動作を見ることにした.
薫Z木家系図の重婚グラフには親子枝が23個登録され,このうち10個がクラスタ23に関わる循環枝(自己ループ)であることがわかった.
- 【#408 @2桐壷院】⇒【#406 @1光源氏】
- 【#408 @2桐壷院】⇒【#488 @42朱雀院】
- 【#410 @3桐壷の更衣】⇒【#406 @1光源氏】
- 【#488 @42朱雀院】⇒【#514 @55落葉の宮】
- 【#488 @42朱雀院】⇒【#518 @57女三宮】
- 【#556 @76致仕太政大臣】⇒【#562 @79柏木】
- 【#624 @110弘徽殿大后】⇒【#488 @42朱雀院】
- 【#656 @126源氏宮】⇒【#518 @57女三宮】
- 【#674 @135致仕太政大臣の北の方】⇒【#562 @79柏木】
- 【#710 @153一条御息所】⇒【#514 @55落葉の宮】
これはかなり予想外の結果だ.これらの枝をすべて除去しないと,この系図の重婚クラスタ循環は解消しない.そのことを考えると薫のZ木家系図で多重カードが3件しか出ていないというのはむしろ驚異と言ってもよい.薫のZ木家系図を再掲してみよう.
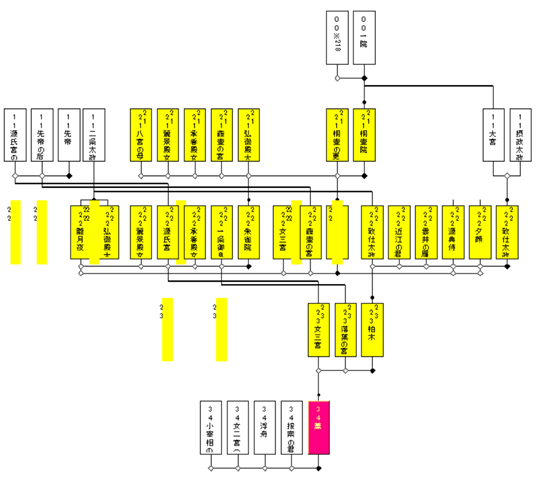
おそらく,この図面で多重カード3というのは極限と思われるが,上の循環枝リストからは3という数字を導出することはできない.考えられるファクタとしては,「世代数」が関わっている可能性だ.このクラスタに関わるノードをすべて色表示してみよう.
クラスタ23に関わる23のカードは3世代の範囲に分布している.このことから推定されるのは,おそらく「クラスタが分布するk世代の範囲に相当する多重カードkの出現は避けられない」ということではないだろうか?最適解と言えるかどうかは分からないが,各世代に高々1枚の多重カードというのは望み得る限界ではないかと思われる.この循環する親子枝10本を解析すれば,このクラスタを展開するのに少なくとも3世代を要するということを立証できるのではないだろうか?もし,うまくゆけば,メンバーをどのように世代配分すれば最適かというところまで分かるかもしれない… つまり,本来なら一世代に収まらなくてはならない重婚クラスタを「世代分割」可能か?という問題として定式化できる.
それを調べるには,やはり次の段階であるハッセ図と呼ばれる階層図の生成手順を見るしかないだろう.ハッセ図(多重グラフ3)は重婚グラフ(多重グラフ2)をベースに構築される.もし,その手続きの中で「重婚クラスタの(多重を最小化する)世代分割」が可能であれば,図面はほぼ仕上がったものと言ってよい.つまり,(多重不可避のカード以外の)すべてのカードの絶対世代番号が確定できるということになる.もちろん,多重が存在しない場合にはすでに目標は達成されている.問題は重婚クラスタ循環が存在する場合にそれが可能か?という点にある.