povo1.0でテザリングするのはやはり,かなりきつい.フレッツ光を使うという手があるかもしれない.フレッツ光なら月額3~4千円で間に合う可能性がある.スマホをpovo2.0に切り替えれば基本料金はゼロになるから,ほぼフレッツの料金だけということになるので,なんとか予算額以内に収まる可能性がある.現在はほとんど外に出ていないし,出るときでもスマホを置いて出かけているので,とりあえずのところそれほど支障もないような気がする.以前はウォーキング中にYouTubeを聞き流ししていたのだが,最近はそのような使い方をほとんどしていない.
とは言え,そのような使い方を今後一切しないという訳でもないので,その場合はそのつどトッピングを購入しなくてはならなくなる.それもかなりきびしいような気がする.USBテザリングを使うともう少し動作はましになるような感じだが,そうすると今度は他のマシンとのインタフェースに支障が生じる.USBテザリングとWiFiによるアクセスポイントの併用はもしかするとできる可能性はある.まぁ,ともかく,もう少し,様子を見ることにしよう.
現在ノート(Dospara)とタブレット2機の計3台を使っているが,そのどれもが終末ホスピスに入っている.いずれも電源投入時の立ち上がりに覚束ないところがあり,いつご臨終となるのかはらはらしている状況だ.2 in 1のミニノート(BlackHawk)はキーボードを外してタブレットとして使っているが,しばしば画面(内蔵モニタ)が崩れて流れてしまう.外付けモニターには出力できるのでハード的にはまだ活きているようだが… 薄型ノート(VAIO2)はバッテリが膨張して背中の辺りが大きく膨らんでいる.使っていないノートなどはまだ他にもあるが,CPUパワーが足りないので予備機としては心もとない.
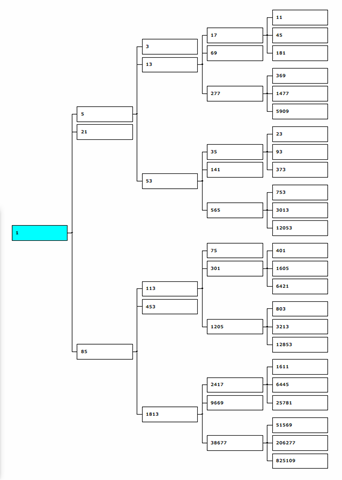
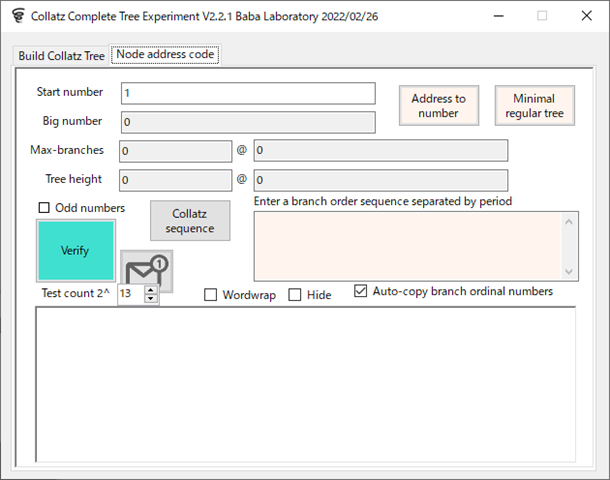
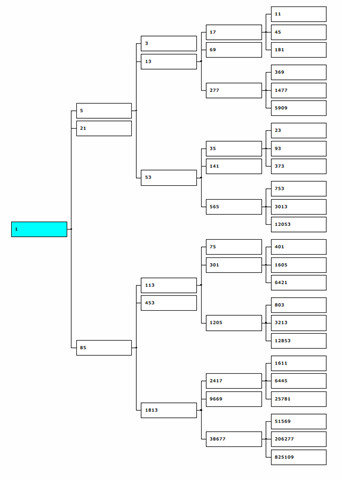
さて,そろそろ仕事に入ることにしよう.どこから始めたらよいか?現状の問題を洗い出して個別対処というのでもよいが,まず,ログを読み直してどこから作業中断になっているのかを確認しておいた方がよい.現在外部公開しているCollatz Tree Generatorのバージョンを確認しておこう.テント村トップの固定ページではV1.1.5となっている.まず,これを基準点と考えなくてはならない.この版には「Build Collatz Tree」と「Get branch position」という2つのタブがある.最初のタブは①ルートノード番号,②枝数,③木高を指定して正則コラッツ木を出力するようになっている.2番目のタブには,①Verify, ②Get the sequence,③Get the number,④Truncated treeのボタン4つ.
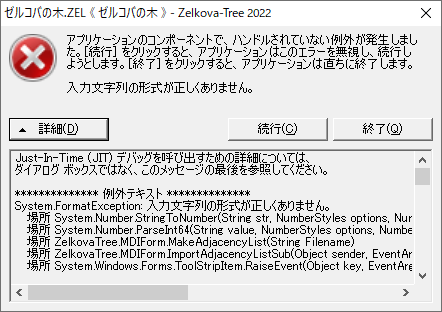
この使い方を飲み込むまでは結構大変そうだ.製作者のわたし自身ほとんど使いこなせない.一応 VAIO2上では動作していることは確認できた.「Collatz Tree Generator」自身が壊れていると考えた大きな理由は,開発機でこの版を動かしたとき,画面が崩れてしまうという問題が出ていたからだ.画面のレイアウトが崩れてTest countの入力ボックスをメール送信ボタンが覆うような配置になっている.この問題は以前から確認されていたはずだが,開発機ではテストを行わないという手順になっていたので忘却していたのだろう.この問題の解決はかなり難しいような気がする.機種ごとにレイアウトを微調整するようなことまではできないと考えられるからだ.おそらく対処するとしても,何か「逃げ」を打つようなことしかできないのではないかと思う.ともかく,障害としてリストアップしておこう.
▲開発機でCollatz Tree Generatorを起動して,2番目のタブでTest Countの入力ボックスの上にメール送信ボタンが被ってしまう
Collatz Tree Generatorのリリース版のバージョンはV1.1.5だが,最新版はV3.0.3になっている.ということはこの中間にV2.0というのがなくてはならないはずだが,どこに置いてあるのだろう?バックアップはすべてどこかにあるはずだが,整理しておく必要がある.⇒すっかり忘れていたが,2022/05/06「二兎を追う者は一兎をも得ず」にこんなことが書いてあった.
ここに来てにわかにもうひとつのミレニアム懸賞金問題が急浮上してきた.例の「数学・物理etc 談話室」で「ケーニヒスベルクの橋の問題」が話題となり,そこでまた大きな進展があったためだ.もう少し詰めないとものになるかどうかは分からないが,感触としては十分な手応えがある.「二兎を追う者は一兎をも得ず」と言われるが,「一石二鳥」ということわざもある.
なんのことを言っているのかさっぱり分からないが,リンクに飛ぶと
(6’)任意の連結な無向グラフ上の奇次数頂点の集合をOとすると,|O|は偶数であるから,Oを2つのパートO1, O2に分けて,(o1, o2)のような奇次数頂点の「ペア」を組んだとき,このようなすべてのノード対(o1, o2)に付き,o1とo2を結ぶ他の奇次数頂点を含まない初等的経路が存在する.つまり,互いに素であるような(共通点を含まない)奇次数頂点ペアを結ぶ経路のセットが存在する
のような命題を提示した上で,「(6’)が成立するとかなりおもしろいと思われるのですが,今のところ確信はありません.「3正則グラフのハミルトン閉路問題はNP完全である」とどこかで聞いたような記憶があるのですが,もしそれが本当なら,(6’)の成立はNP=Pを証明したことになるかもしれません.」としている.多分,このことを言っているのだろう.いまは,そこまで突っ込む余裕はないが,ヒマができたらもう一度調べてみる価値はあるだろう.
コラッツ木生成ツールの出力ファイルにADLという拡張子を持ったものがある.この拡張子が何を意味しているのかさえ忘れてしまった.「極小反例サンプル抽出」というのを行おうとしているようなのだが,「極小サンプル」とは何かすらも覚えていない.この時期にはゼルコバの木のデバッグも並行して実行している.「スタックオーバーフロー」などの障害も発生しているが,解決しているのだろうか?コラッツ木生成ツールが生成したCSVファイルをインポートしたとき,一部ノードが消失してしまうような現象が出ていたが,この辺りの問題なのではないだろうか?開発環境としてはVS2019を使っているが,VS2017の修復インストールなどのこともやっている.
2022/05/03のタイトルは「あきらめてここで打ち切るか,何か対策を考えるか?それが問題だ」となっている.どうも,ここで「あきらめて打ち切り」の状態で終わっていたのではないだろうか?ここでは,12243点というゼルコバの木のスケールを超えたサンプルを扱っているのだが… 障害の原因はメモリ不足にあるように思われるのだが… Windows 10とWindows 7という開発環境の違いも影響しているようだ.「極小反例サンプルの抽出」ではUNDO機能を使って何かやっているようだが,それもよくわからない.2022/04/28「LNK1248: イメージ サイズが最大許容サイズ (80000000) を超えています」には,
先祖ノード(とその配偶者)だけは例外的に結婚枠の中に入っていないが,これはいま考えると敗因だったような気もする.⇒おそらく,この「コラッツ特注版」の挑戦が完結した時点でここに戻ることになると思う.「コラッツ特注版」は「単純な木」であり,「結婚木」も「単純な木」と考えられるから,「系統並び替え」を「もっとも単純なトポロジーソート」として再編成できるはずだ.
ともある.「ここに戻る」というときの「ここ」が何を指しているのかもよくわからないが,「先祖ノードを結婚枠内に収容すること」を意味しているのだろうか?コラッツ木生成ツールのタブにはA面,B面という名前が付いている.B面は3機能(コラッツ数列,アドレス変換,幹線木)+検証テストという構成だ.「極小反例サンプル抽出の自動化」という技法が何を意味しているのかまだよくわからないが,2022/04/26「極小反例を探す長いジャーニーが終わった」では,「応用が効く」としているので,なんらかのデバッグ技法になっているのだろう.
UNDOに関してもかなりの修正が入っている.2022/04/16は「Windows 11をダウングレードしてWindows 10に戻す」となっている.開発機にはWindows 11をインストールできたようだが,動作不良が起きたため元に戻している.Windows 11への移行はどこかの時点で実行しなくてはならないかもしれない…
2022/04/16の記事に「極小反例サンプル抽出の自動化」の目的と方法が書いてある.ループカウントオーバーなどの障害が発生したとき,その障害を再現できる最小構成のサンプルを抽出するという課題だ.実装がどうなっているのかはわからないが,多分コンパイルオプションとして作り込んでいるのではないかと思う.⇒VBの「包括自動テスト」に組み込んで,メニューから起動するようになっている.⇒「検索文字列.TXTが見つかりませんでした」というエラーに関しての記事がある.
ADLという拡張子は「隣接リスト専用」として設置されたもので,タブ区切りのCSVファイルだが,中身は隣接リストという特殊フォーマットだ.ADLはActivities of Daily Livingで「日常生活動作」という意味だという.まぁ,もちろん,元の意味は adjacency listということだったのだろう.ADLファイルはZELファイルと同様にダブルクリックで開けるようになっている.これは系図データではない「一般のグラフ」をゼルコバの木で扱えるということを意味している.
2022/04/11から「コラッツ木生成ツールから直接ゼルコバの木を起動する」ことができるようになっている.2022/04/06には「『拡張コラッツ問題』は一般には成立しない」という記述がある.これはコラッツ予想問題に直接関連する考察だ.今回の課題になっている「Kurmer Sultanの独創的解法」に関係があるかもしれない.
前稿(2022/04/06)には,2つの式が記載されている.
ノード番号:={長子ノード番号}.{兄弟順位} (1)
長子ノード番号:={親ノード番号}.{長子識別子} (2)
これら2式が正しければ,
ノードN:={地番1}.{地番2}.{地番3}…{地番k}
のようなアドレスコードが可能となり,すべての自然数はその内部にコラッツ木の(暗号化された)アドレスコードを持っているということになると予測される.
としている.これから,
拡張コラッツ問題:kを任意の奇数(定数)であるとする.任意の自然数Nについて,Nが偶数ならば2で割り,奇数であればk倍して1を加える操作を反復すると,かならず1に帰着する
という設問が提示される.ただし,①k=1の場合は自明,②k=3はコラッツ問題に相当,③k=5では成立しないところから,
そもそもk>3の場合に,「長子木」のようなものが構成可能であるかどうかは,まったく自明ではない.というか,おそらく,k>3の場合には「長子木」のようなものは存在していないのではないだろうか?逆に言えば,長子木のようなものが構成可能であるのは,k=3の場合に限定されるのではないだろうか?いずれにしても,「長子木とは何か?」ということが追求されなくてはならないだろう.
としている.コラッツ問題に関する考察に関してはおそらくここが我々の最終到達地点である.コラッツ生成木ツールの仕様は変遷しているが,完全木と仮想木のどちらが優位か?という問題で紛糾している.目標は,自然数Nをデコードして一般コラッツ木のアドレスコードに自動変換することである.2022/04/05では『「三本桜の復活」→「銀河系の再構築」』としているが,これは何だろう?⇒コラッツ木から3倍数を除去したものを完全木と呼んでいる.3倍数は終端ノードになるため,完全正則木を構成することができない.このため,アドレスコードが変則的なものにならざるを得ないので,これを除去した木を考えて完全木としているのだろう.
しかし,3倍数を除去することによって生じるコラッツ木上の空位とアドレスコードの対応は必ずしも自明ではない.仮想木の場合は仮想木上の位置とノード番号の関係は明確に定義されているのでむしろ対処し易いのではないか?と考えられたので急遽方向転換し,汎用アドレスコードを仮想木上で再定義することにした.
としている.Sultanはこの逆に3倍数を基準にすべてのノードをコラッツ木に配置するという戦略を取っており,我々と真逆の方法論になっているように思われる.この記事では「コラッツ木上で共通の親を持つノードを兄弟ノードとし,兄弟ノードのうち最右に位置するノードを長子ノードとする 長子ノードはコラッツ数と呼ばれることもある」としているが,Sultanは確か,非3倍数であるような(すべての)奇数をコラッツ数と呼んでいたような気がする.※
仮想コラッツ木はグラフの連結性を維持しながら,兄弟ノードを長子ノードに合併・縮約することによって得られる一般コラッツ木の簡約グラフである 仮想木上の(1を除く)すべてのノードは長子ノードである
これで見ると,「仮想木」というのは,「長子木」に他ならないように思われる(仮想木から1を除去したものという別定義もある).これに対し,「拡張コラッツ木」にはすべての自然数が含まれるようだ.「仮想木検定」というのがCollatz Tree Generator V2.0に与えられた名前であるように思われる.「コラッツ銀河高速道路系プロジェクト」というのがそれに該当する.この最終版はCollatzCoreTree 2022-02-22-1の一つ前のバージョンと思われる.CollatzCoreTreeというプロジェクトからバージョンをV3.0.1に切り上げている.「仮想木で汎用アドレスコードをサポートする」というのが,このプロジェクトの目標だ.「完全正則木」を考えているのは,「証明」に備えるためと考えられる.(長子木は完全正則木である)
※「コラッツ数」は2022/03/29には以下のように定義されていた.
『コラッツ木からすべての3倍数を除去したグラフをコラッツ完全木,コラッツ完全木上のノードをコラッツ数とする』
これはSultanの定義と完全に一致する.ようやく「コラッツ国の公用語は4進数である」というところまで来た.ノード番号を16進ではなく4進表記すると,
兄弟ノード番号=長子ノード番号+1の並び
のようになる.このとき,子ノード番号をNとして,3N+1を2進数表記してやると,
子ノードNの3N+1バイナリ表現=親ノードのバイナリ表現+0の並び
となるが,これを3進数表記したらどうなるか?というところに興味がある.その準備として「横書き」機能拡張が導入された.Core Treeというのは「コラッツ中核木」=3倍数を含まないコラッツ木である.
2022/03/25「非公開投稿」では,ロギング用のノートの配置をいろいろ試している.結局,「ロギング用のノートは左配置しかない」ということになったのだが,今回も多少の改善を試みて,下図のような配置に落ち着いた.最左のタブレットとモニターの中間にあるのがロギング用のタブレットだ.モニターにはタブレットの画面が表示されている.これまでで一番安定した配置になったような気がする.
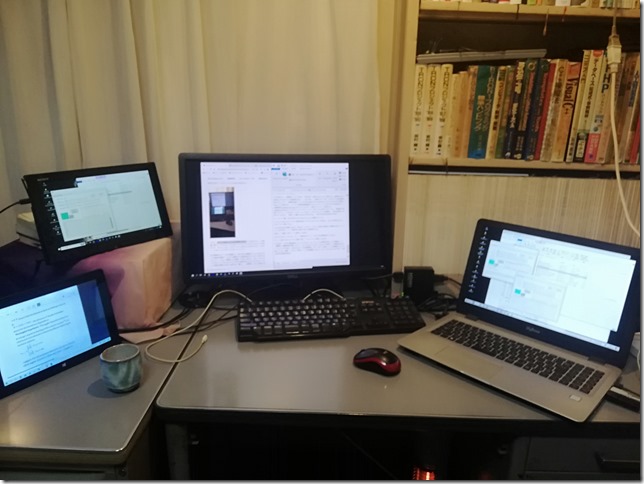
いや,これは基本的に2022/03/17の配置とまったく同じだ.