投稿者: babalabo

フロック類という概念は導入されたものの，極大部分群検定の進捗は思わしくない．まだフロックグラフというものをうまくハンドリングできていないように思われる．どうすればよいか？フロックリストは群を生成した時点で作られるもので，不変と考えられるから動的な変化はフロック表に反映されなくてはならないだろう．フロック表はループカウントごとに作り直しているのだから，完全なものができなくてはおかしい．つまり，削除されたフロックの分小さくなっていなくてはならない．フロック表はフロック数を基準に生成されているが，これを実態を反映した動的なものに変える必要がある．

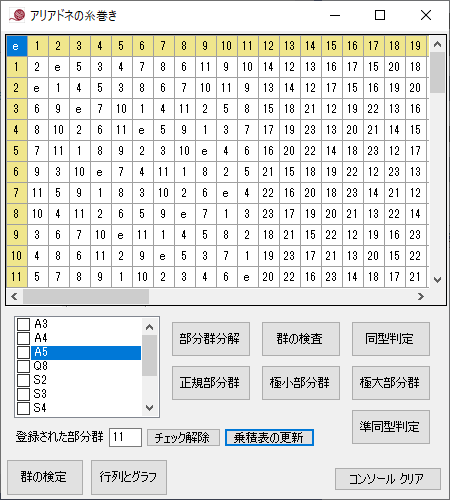
フロックという整数配列でフロック番号とインデックスの変換ができるようにした．また，フロック現数というパラメータでカウントを押さえるようにしたので，正確なコントロールができるようになっているものと思われるが，成績は芳しくない．A4では位数4を一つ，A5では全滅している．群A5は57個の真部分群を持つ■ 位数2X15 位数3X10 位数4X5 位数5X6 位数6X10 位数10X6 位数12X5．少なくとも位数12の部分群は取り出せなくてはならない．

A5:<1,3> 位数12という部分群を見ると， [0,5,5, 0,22,22, 0,29,29, 0,15,15]となっているので，{0, 5, 22, 29, 15}という５つのフロックから構成されていることがわかる．{e,5,9, 14,22,49, 55,51,29,  33,24,15}という構成なので，{1,2,3…}などの削除から入れるはずなのだが… フロックが参照する枝数が少ないなどの条件は部分群を構成するための十分な条件になっていない．同等のフロックがいくらでも存在し，それらを区別する理由がない．

結局，総当り検査をするしかなくなってしまう．温存されるべきフロックとこの[5, 15, 22, 29]には何か特異な点はあるだろうか？あるいは，これらの４フロックを結びつける何かの動機はあるだろうか？合計ではなく，最小枝数で見たらどうなるか？⇒どうもうまくゆかない．F16が真っ先にカットされるようだ．何かよほど巧妙なシナリオを考えないとうまくゆかないと思う．そのシナリオを書く素材が見つからない…２つのフロックF1, F2があるとき，F1F2=F3と言えるだろうか？

A4でフロック数=5, A5では23，S5では48になる．S5で48なら大したことはないように思えるが，もし総当りが必要ということになると，A4で2^5=32，A5で2^23=8388608，2^48= 281474976710656ということになり，尋常な話では済まなくなってくる．せめて，最大の部分群だけでも取り出せればよいのだが…

群の元集合をフロックと呼ぶ類に分割することができる．すでに実装して動いている．ほぼ完璧と言ってよい．あとはこれを極大部分群と極小部分群の検定に組み入れるだけだ．まず，極大部分群検定から始めよう．極大部分群検定では，フロック１個を削除したところから始めて，群になるまで繋がりのある元をフロック単位で削除するという操作になると考えられるが，この場合，乗積表に空いた穴を塞ぐために元対のどちらをカットすべきかという問題は残るような気がする．確かにフロックを一括解除しているので収束は早まるとは思われるが…ともかくフロックをまとめて解除するところまで作ってみよう．

フロックという同値類を導入したにも関わらず，極大部分群分解はクリーク分割問題になるというところは変化していないように思われる．最大のメリットは群グラフが簡約されて小さなものになっている点だけだ．ともかく，フロックを点とするグラフ＝フロックグラフを書いてみるしかないのではないか？フロックグラフを描くためにはまず，その隣接行列が必要だ．これをフロック乗積表と呼んでおくことにする，

▲何かの理由でコンソールが『詰まる』場合があるようだ．画面がフリーズして何も操作できないので，コンソールに文字入力したら突然動き始めた．

クリーク分割問題が解ければ極大部分群検定は解ける．しかし，クリーク分割問題はNP困難であり，NP完全と同等かそれ以上に難しい問題として知られている．しかし，極大部分群検定には一般の場合と比べいくつか有利な点があるので，それらを利用すればより効率的な解を得られる可能性はあると考えられる．解法を定式化してみよう．

1. 群の乗積表はグラフの隣接行列とみなすことができる．このようなグラフを群グラフと呼んでおこう．群グラフはすべての点が繋がっているので，つねに完全グラフである．一つの乗積表を共有する部分群グラフが完全グラフであれば，そのグラフの頂点は群を構成する．
2. 単位元はすべての部分グラフに共通し，必ず存在することが予定されているので，グラフから当初から除外して考える．つまり，群グラフは最大でもN-1点グラフである．
3. 群には溶接された硬結な結節点が２種存在する．一つは逆数関係による固着，もう一つは自乗巡回路である．これらは一つの点を除去するとすべての点を除去するしかなくなるので，１個のブロックを形成している．従って，これらの元を合併して一つの点とみなすことができる．
4. 今後はブロックを点に簡約したグラフを主に考える．これを簡約群グラフと呼んでおくことにしよう．また，以下ではブロックを簡約した点をフロックと呼ぶことにする．
5. 簡約群グラフから頂点（強連結成分，flock）を一つ取り除いたグラフ上で最大の完全部分グラフ（クリーク）を見つけることがテーマとなる．
6. フロックAを取り除くと，他のフロックBに影響する．x∈A, y,z ∈Bでx=yzであれば，xの除去によってy ないしzの除去が発生し，その結果フロックB全体が除去の対象となる．従って，Aを除去することにより，フロックBもドロップする．
7. この操作をドロップが生じなくなるまで反復して得たグラフは連結した完全部分グラフであり，それらの元集合は１個の極大部分グラフを構成する．
8. 極大グラフ検定はすべての個別フロックについてこれを反復することで完了する．つまり，フロック個数分の極大部分グラフ（おそらく同型のものを含め）が生成される．
9. フロックはブロックではあるが，群ではない．最小のフロックサイズは１で，この場合は x^2=x であるか x^2=e のどちらかである．このようなフロックはローンウルフと呼ばれる．
10. フロックはフロック番号によって管理される．フロック番号は群の生成時に決定され，元表に記入される．フロック番号はフロックの代表元の元番号であり，１以上の飛び番である．
11. フロック数とフロック代表番号のリストは群で管理する．
12. フロックは元集合の排他的な直和であり，群の集合配列を使って生成する．
13. 極小部分群分解では個別ノード単位ではなく，フロック単位で分解を行う．
14. 極大部分群分解では，フロック単位に元をドロップすることで部分群を構成する．
15. このアルゴリズムが確立した後は自乗リスト（べき表）は不要になる．また，元の必須という属性も不要になる．
16. ローンウルフを放置しておくと面倒くさいので，実装では一括して単位元の預かりとすることにした．

これで完璧なアルゴリズムが確立した．現行論理をこのアルゴリズムでカバーするのは難しくない．⇒極大部分群検定に入る前に，まずフロックの概念が正しいことを検証するためのコードを書いておこう．フロック元分割という関数を作って群のコンストラクタから呼び出すようにしてみたところ，驚くべき結果が出た．Q8の場合すべての元が一箇所に集まってしまう．こんなはずではなかったのだが… いや，やっていることが間違っている．最初にやるべきことは元とその逆数を一元化することであり，べきの関係ではない．

元表をダンプできるようになったが，元の構成を再考してみたい．現行では元.置換表示に置換積を格納するようにしているが，むしろ，置換そのもの（全単射）の方がよいと思う．応用が効くし，乗積表から置換を割り出すとすれば置換の形式になると考えられるからだ．メンバー名も置換表示ではなく，置換でよいと思う．置換プリントで置換積に変換することができる．⇒ただし，データ型が違う．stringの配列だ．置換はいくらでも大きく取ることはできるが，現状ではたかだか７程度なので，MAXを押さえておくことにしよう．

暫定的にｃMAXPERMARRAY=７としておく．この定数はPermutationクラスで持つことにしよう．しかし，置換を置換積の形式に変換するのは結構厄介な計算になる．現物の置換の他に，恒等置換の文字列並びが必要だ．置換積への変換という関数を作った．⇒もうひとつ手当しておくことがある．元表はソートされることがあるので，個別の元に番号を付与しておく必要がある．さて，もう一度極大部分群に戻ろう．やることはすでにわかっているので，後は実装するだけだ．

▲A5の部分群検定で(Count != 部分群数)で停止した．これは昨日S5で起きていたのと同じだ．部分群数は58，Countは60になっている．極大部分群数が加算されている．現行では部分群検定に極大部分群検定は含まれていないので外しておこう．⇒解消した．

▲時間の掛かる処理ではカーソルを砂時計にする．

かなりよい動きになってきたが，まだ完全ではない．特にA4，A5に不審がある．A4，A5では位数3×2を検出しているが，A4の部分群には位数2X3 位数3X4 位数4X1がある．A5は正規部分群は持っていないが，57個の真部分群がある．位数2X15 位数3X10 位数4X5 位数5X6 位数6X10 位数10X6 位数12X5だ．A4は位数4の正規部分群を持っている．極大部分群と正規部分群はかなり近いような印象があるが，A4の位数4の正規部分群を検出できていないのは問題だ．

☆「A5の部分群 ハッセ図」でググったら，１３番目にテント村(2023/11/13)が出てきた．投稿からまだ一週間しか経っていない！ハッセ図を出したいのだが… ゼルコバの木で表示することは可能だろうか？ゼルコバの木はハッセ図を描くようには作られていないが，ある程度それらしきものは出せるのではないか？ハッセ図を見ながら考えればかなりわかり易くなると思われるのだが… 群（部分群）をノードとし，部分群の包含関係を親子関係と見立てればハッセ図になるような気はする．ただし，そのためにはすべての部分群をキープする必要がある．現行ではそうなっていない．同型な部分群は代表群を一つ残してそれ以外は破棄されている．A4では8個だが，A5では57個もある．

▲現行では群をダンプするとき，元の集合{}の形式で表示しているが，これを元の置換積表示でも表示できるようにする．⇒部分群の登録のところでは生成元を置換積表示している．

▲ストック部分群と同型で追加されなかったときは，既存ストックの部分群名を表示してほしい．⇒対処した．

ともかく，極大検定でA4の位数4の部分群(=V)が取れない問題を調べなくてはならない．A4={a, b,…, l}のような元を持っている．V={a, d, i, l}なので，落とされているノードは{b, c, e, f, g, h, j, k}の８個だ．手順からゆくと真っ先に落とされるのはｂだが，そこから先の動作をトレースしてみよう．

★★★★登録解除：i=1 peel=b count=0 N=12 台集合=12
登録解除 count=1 N=11 x=b
登録解除 count=1 N=10 x=c
■■■■元対解除：i=1 peel=b 元対=(3, 6) →3 d
登録解除 count=1 N=9 x=d
■■■■元対解除：i=1 peel=b 元対=(4, 9) →9 j
登録解除 count=1 N=8 x=j
登録解除 count=1 N=7 x=f
■■■■元対解除：i=1 peel=b 元対=(4, 7) →4 e
登録解除 count=1 N=6 x=e
登録解除 count=1 N=5 x=g
■■■■元対解除：i=1 peel=b 元対=(7, 8) →8 i
登録解除 count=1 N=4 x=i
■■■■元対解除：i=1 peel=b 元対=(7, 11) →11 l
登録解除 count=1 N=3 x=l
■群A4:～b 位数3〈～b〉 素群 極大 可換 巡回 自己同型 {a,h,k}

削除される順序は，{b, c, d☓, j, f, e, g, i, l☓}となっている．最初のつまづきの石はｄだ．競合しているのは{g}だ．gを削除するのが正解であるところ，間違ったカードを引いている．ｄはx^2=dとなるノードがない．つまり，べき表では(0, 0)となっている．ｇは(1, 4)だ．この点でｄが選択されているが，ｄのべき先は0つまり単位元だ．しかし，単位元の位数が2になっているというのはおかしい．ベキがeとなるとき，つまりx^2=eのときは位数2としているためだ．間違い易いので単位元はループの外で設定することにしよう．単位元の位数は１であるとした．

競合元対：x=3:d #2 (0, 0=a #1) y=6:g #3 (1, 4=e #3)

べき元が０ということは乗積表の対角線上にそのノードが現れないことを意味している．これはその意味では削除し易い条件のようにも思われるのだが，単位元に直結している位置でカットしたら根こそぎ倒されることは間違いない．この意味では最優先されるのは位数ということになる．書き直してみよう．⇒修正して以下の結果になった．

■群A4は3個の極大部分群を持つ■ 位数2X2 位数4X1
■群A5は3個の極大部分群を持つ■ 位数4X1 位数6X1 位数10X1

A4は8個の真部分群，位数2X3 位数3X4 位数4X1なので，まぁまぁというところ．A5は57個の真部分群，位数2X15 位数3X10 位数4X5 位数5X6 位数6X10 位数10X6 位数12X5 なので，まだまだだ．位数12が出てこなくてはならない．

▲S4～bをダンプしようとして例外が起きた．置換構成が空だ．⇒チェックして空テキストで補充するようにした．

極大部分群検定の書換えを進めているところだが，その前にやや大仕事になってしまうが，元のオブジェクト化というのを片付けておくことにする．現行では元は台集合に格納された名前だけで管理しているが，これを独立のオブジェクトとして管理しようという発想だ．これができるとさまざまな元の属性を一元管理できるようになるのでかなり都合がよい．また，元の位数などの新しい属性の追加も容易にできるようになる．おそらく現在使っている部分集合[,]などは廃止できるようになると思われるが，当面は並立のままとしておこう．置換リストのダンプも元表のダンプに代わるはずだ．

▲Q8の極大部分群として位数4の部分群を２個取り出すことに成功したが，「j」を除外した部分群が出てこない．i, k と条件はまったく同じであるはずなのだが… いや，i と k は出ている．おそらく，ブランクセルの解決で同型部分群を引いてしまったのだろう．

どうもなかなかうまくゆかない．ブランクセルの元対を２つに分けてそれぞれで検定するようにしてQ8の場合だけは解けたが，それ以外ではまったく無力だ．再帰的に下降してすべての場合を尽くせばこの方式でも解に到達することは不可能ではないが，コストが掛かり過ぎる．削除対象ノードの逆元を削除するという方法はまだ試していないのでやってみる価値はあると思うが，その前に群のコンストラクタで位数と逆元および自乗元を拾い出しておくことにする．これをやっておくといろいろ便利なことがあると思う．

▲A5の極大検定を実行して，乗積表[32, 32]が空になっている．⇒群表に穴が空いている．群の再構成でエラー復帰するようにした．

▲Q8の部分群検定→群の検査で例外が発生した．⇒N=4のところ，元集合は1しかない．⇒部分群検定のように元が逐次追加されるような群ではあらかじめ元集合も大きめに作っておく必要がある．⇒対処した．

▲S5の部分群検定で(Count != 部分群数)で停止した．

巡回群の生成に移ることにしよう．巡回置換の元は(a1, a2, …, am)の形の置換であると考えられる．従って，元の個数はmで置換リストの長さと同じはずだ．事例を見てみよう．⇒上記の定義で問題ないと思う．⇒実装した．一応動いているが，群の検査の表示が少しおかしい．すべて合成群になっている．また，C4は巡回群ではないとされる．群の属性ではデフォルトが合成群になっているので，合成群と出てくるのはとりあえず，やむを得ないかもしれない．巡回群であっても必ずしも素群であるとは限らないはずだ．

▲C4の群属性がおかしい．非巡回群となっている．⇒ecountがインクリメントされていない！⇒修正した．

巡回群の生成はおおむねうまくいったようだ．少なくとも位数が素数であれば，すべて巡回群であり，かつ素群であるとしてよいのではないか？⇒これで，少なくともC2, C3, C5に関しては「素群」表示が出せるようになった．今のところ，部分群分解をしないと素群であるか否かの判定はできないようになっているが，非自明な部分群を持たないことが判明した時点で属性を「素群」とすべきだろう．ないし，極小部分群検定でそれをやってもよい．

▲Q8<i>が素群になっているが，分解できる．これはまずい．⇒現行では極小部分群で抽出された部分群はすべて素群であると推量しているが，どうも間違っているようだ．Q8<i>はQ8の部分群ではあるが，極小ではない．これはかなり困ったことだ．追加登録の論理を見直さなくてはならない．⇒いや，論理を見直すのではなく，用語の定義を見直すことにする．素群というのは部分群に対する定義ではなく，群に対する定義であると考える．つまり，分解できない群が素群である．

極小な部分群というのはある群の部分群についての定義であり，「極小な部分群とはあるノードを含みそれ以上ノードを減らすと部分群でなくなるような部分群」とする．同様に，極大な部分群は「あるノードを含まない部分群でそれ以上ノードを追加すると部分群でなくなるような部分群」であるとする．つまり，正規部分群などと同様「部分群としての属性」である．これなら現行論理のままで行ける．ただし，極小と極大という属性を追加しなくてはならない．

正規部分群は共役変換検定というテストで判別できるが，極小・極大はおそらく極小/極大部分群の抽出によってしか検出できないのではないかと思う．これは仕方ないだろう．素群の反対は合成群だが，極小ないし極大と素群は並立するだろうか？素群で極小でないということはあり得ないが，極小で素群でないということはある．また素群で極大ということもあるのではないか？⇒極大部分群検定は極大部分群の抽出に改めた．大分正確になったのではないかと思う．

いよいよ，極大部分群検定だ．

▲これまで素群と表示していたところを極小部分群に改める必要がある．⇒素群数を極小部分群数に一括変換した．素群数が必要な場合は別途集計する必要がある．

既存の極大部分群検定はリネームして別途立て直す必要がある．多分，極小部分群の抽出の逆操作になると思われる．⇒追加登録は引数で群Gを渡している．登録解除はGの上で操作している．これはまずい．追加登録と登録解除が双対になるように作り変えるべきだ．

ボタンの配置を変えたはずなのだが戻ってしまっている．なぜだろう？どこかでバージョンが入れ替わってしまったのだろうか？⇒バックアップにも残っていない．作り直すしかない．

この方が使い勝手がよいと思う．部分群分解・正規部分群が並び，極小・極大を並べて群検査と同型判定を右手に配置した．

正規部分群の集計に不審な点がある．見直しが必要だ．Q8は４個の真部分群を持っている．#2×1, #4×3．リストにはこのうち，Q8:<-1>とQ8<i>が登録される．Q8は４個の非自明な正規部分群を持っている．Q8:1，Q8:2, Q8:4, Q8:6．最初のQ8:1は位数2，それ以外は位数4で，これらは部分群分解の結果と一致する．ここで，Q8:1とQ8:2を登録しようとしているが，登録済みであるため新規追加された部分群数=0となっている．これらの動作はおおむね正しい．

従って，問題は◎群Q8は4個の非自明な正規部分群を持っている 位数2X2 位数4X6というところのみと考えられる．これはおそらくsubGNで重複カウントしているためだろう．部分群の追加で一律subGNをカウントアップしているところに正規部分群で再カウントしているためだ．subGNは発生点でカウントアップするようにした方が間違いがないと思われる．⇒対処した．動作しているようだ．

▲極大部分群検定は仕掛りとなっており，まだ仕上がっていない．Q8の極大部分群検定では位数2の巡回群が極大とされているが，それ以外は見落とされている．位数２の部分群が極大というのはそれ自体誤りであるように思われる．A2, A3, A4は極大部分群を持たないとなるが，これもおかしい．A3は巡回群であり，素群であるから極大部分群を持たないというのは誤りではないが… 極大部分群を持たない⇔自明な部分群を持たないでなくてはならない．

▼正規部分群はあるノードを含む部分群として生成されているので，生成元を特定できるはずだ．部分群名称の命名規則を統一した方がよい．しかし，seedが同じでも同一群になるとは限らないのではないか？たとえば，A4では(3)[8]⇒〈d,i〉{a,d,i,l}は位数4のA4の合成群(正規部分群)となっているが，正規部分群検定ではそこまで解析できないのではないか？⇒暫定現状のままとする．

▲A4の正規部分群のカウントがおかしい．◎群A4は2個の非自明な正規部分群を持っている 位数4X1と表示されているが，正規部分群は１個のはずだ．⇒正規部分群数が初期化されていなかった．

▲S4で部分群分解のあと，正規部分群で追加が発生している．⇒これは多分そういうルールになっているためと思われる．位数4のS4:7が追加されている．しかし，位数12のS4:3は正規部分群だが追加されていない．S4で位数4の部分群には<j>と<b,g>がある．位数12は<d,h＞{a,d,e,h,l,t,x,u,p,q,m,i}だ．S4-3の台集合は{a,d,e,u,p,l,t,m,i,h,q,x}で<d,h>と一致するが，S4-7の台集合{a,h,q,x}は S4:<h,q> #4〈h,q〉{a,h,q,x} とは一致するが，登録された#4の部分群とは一致しない．これはこれでよいとするしかないのではないだろうか？⇒とりあえず，よしとしておこう．

ここまで来ると極大部分群検定の未整備が目立ってくるので，取り掛かることにする．いまのところ極大部分群検定は一部の場合にしか適用できないが，すべての群を対象とするように改修しなくてはならない．それにしてもQ8で位数2の極大部分群というのはかなりおかしいので，まずここを見ておこう．⇒この動作はルールに沿ったものになっている．つまり，べき表でy^2=xとならないｘを削除するというルールだ．x=y^2となるのは，1と-1だけなので，この２つだけが残って「極大部分群」を名乗ることになる．つまり，現在の極大部分群検定は原理的に破綻している．というか，仮に適用できたとしても限りなく狭い範囲にしか適用できないように思われる．

確かに，S5やS4などには適用できているのだが… どういう場合に適用できるのかを見極めるのはかなり難しいような気がする．その前に部分群のソートを片付けてしまおう．ソート後は，部分集合，部分群生成元，生成元，可換群は無効になってしまうので，とりあえず null を格納しておく．⇒群の検査の中ですべての属性をチェックするように整備したが，部分群検定では群の検査が呼び出されていない．

▲Q8の極小部分群検定では<k>は極大部分群と表示されるが，ダンプでは素群となっている．この表示は部分群検定で出している．カウントが間違っている．１を足し込む調整が必要．

▲A3の極小部分群検定で■群A3はの後が続かない．⇒対処した．

◆ボタンを押して置換リストをダンプするようにしておこう．⇒出せるようになった．下図↓

大体使えるようになったのではないかと思う．いよいよ極大部分群を詰めるというところではないだろうか？何かやり残しはあるだろうか？可換群など不要になった変数もあるのではないか？一応バックアップを取ってからにしよう．部分群生成元も廃止してよいのではないか？個別の群に置換表示というパラメータがある．巡回群判定，可換群の検査，自己同定検定，共役変換検定も群の検査一箇所で行えばよい．⇒対処した．もう一つ，巡回群の生成というのがある．これは明日やろう．

★共役で同型でないというサンプルはあるだろうか？

GridViewで乗積表を表示できるようになると使い勝手はかなり向上する．大きなテーブルが広がっているコンソールには見たくない．この際，久留島喜内の道具箱を丸ごとC#にインポートすることも考えてみたが大仕事になってしまうので，やや後退して，とりあえずC#に変換済みのForm2のコードを参考に，現状で乗積表を主画面に表示することにする．べき剰余マトリックスではテーブルをいろいろ加工して表示しているが，いまのところプレーンなテーブルが表示できれば十分だ．

喜内の道具箱の使い方まで忘れてしまった．このツールではマトリックスを２枚開けるようになっている．片方は「べき剰余マトリックス」，もうひとつは「べき乗進数表示マトリックス」と表示されている．おそらくこれは仕掛りになっている「加納の定理」と関係するものだろう．いずれ，ここにももう一度立ち返らなくてはならないが，とりあえずパスして先に進むことにしよう．

MatrixⅠのボタンを押したときの動作が分かればよい．BulldMatrixClickではBuildMatrix→BuildPowerGridが実行される．BuildPowerGridに引数で渡されるのはMatrixクラスのインスタンスでこの中にはいろいろな情報が入っているが，配列そのものはInt64の２次元配列だ．配列の行/列数とグリッドの行/列数は指定できる必要がある．いや，これらは現物の配列を直接参照して取り出すこともできる．配列とマトリックスはつねに同サイズでよい．従って，BuildPowerGrid だけ見ておけば十分だ．⇒一応出るようになった．⇒少し手直しして下図になった．

左端の行ヘッダが余分だ．非表示にはなっているのだが，これを消す方法はないものか？⇒できた！デザイナ画面でRowHeadersVisibleをFalseにして消せた．完璧だ．もはや言うことなし．

とりあえず，これ以上の機能は必要ない．A5くらいになると描画までにかなりの時間が掛かるが小さい乗積表なら即座に出る．

それにしても時間が掛かる！S5の乗積表が描画されるまでに１分近く掛かっている．なんとかならないものか？⇒BindingSourceというのを使うと高速化できるという記事があった．

https://qiita.com/belre/items/4650c68ef932acbc597e

使わないときには2873ms掛かったものが，使うことで9.4msになったと言う！AutoSizeModeもNotSetなどにすべきとある．確かに列幅を固定すると一瞬で描画できる．ただし，列幅を指定する方法が見つからない．以下で設定できた．列ごとに幅を設定する必要がある．

for (j = 0; j < n; j++) matrix.Columns[j].Width = 24;

この環境では精々S5くらいまでしか扱えないが，S5で120だからこれで十分間に合う．乗積表は一応これで完成としておこう．かなり気持ちがいい．もうひとつの改善点として，部分群をダンプして表示したい．つまり，部分群配列をソートしたい．現状，部分群のダンプでは素群と合成群の別も表示されていないが，これらも出してみたい．正規部分群/巡回群の別も出すべきだろう．群クラスにはこれら属性を格納しておく場所がない．群属性という項目を設けてビットを立てることにしよう．

群クラスの変数のうち，べき表は参照されていないので廃止できる．最大部分群も部分群検定の中でしか使用されないから廃止でよい．これは極大部分群検定の結果を反映することを考慮したための措置だが，とりあえず切り離されているので廃止とする．最大極大部分群というのも使われていない．subGN，可換群，部分集合などもローカル化できるような気がするが，保留としておこう．属性には以下が含まれる．

1. 可換/非可換
2. 巡回群/非巡回群
3. 正規部分群
4. 素群/合成群
5. 単純群

群.親群は群のコンストラクタで設定するように仕様変更した．親群が判明すれば群の検査の中で正規部分群の判定ができる．

▲正規部分群検定で　◎群Q8は4個の非自明な正規部分群を持っている 位数2X2 位数4X6　のように表示されるが，あまりよくない．正規部分群に限定したカウントを表示した方がよい．⇒どうも怪しくなってきた．Q8の部分群は４個で，#2×1, #4×3と表示されているが，正規部分群検定では８個の正規部分群を持つとされ，#2×2, #4×6のように表示される．⇒正規部分群検定では同一判定をやっていないのではないか？同一群判定は部分群の追加と部分群検定ではやっている．

これはどうも部分群の追加操作に誤りがあるように思われる．正規部分群検定では部分群の追加を実行した後に，正規部分群数を更新し，部分集合やsubGNを書換えているが，この操作は怪しい．極小部分群ではそのようなことはやっていない．極大部分群でもそのようなことはやっていない．部分群検定でもやっていない．明らかにこれはおかしい．これは明日見ることにしよう．来訪者カウントが１６万を超えた．何はともあれ，おめでたいのではないか？

かなりいいところまで来ている．ツールとして十分実用になるレベルだ．同型判定に自信が持てるようになってきたので，群の検査を充実させれば次の課題である共役に移れそうなところまで来ているが，素群についてもう少し知りたいので，極大部分群と並立して極小部分群検定というのを導入しておくことにする．極小部分群というのは我々の用語では「素群」を意味するが，ここでは一般的な用語を使っておこう．

▲また，Console.WriteLine(“\n★極小部分群検定：”+Form1.Group.名称);でハングしている．タイミング的なものが関係しているのだろうか？今度は動いている．

極小部分群分解は一応動くようになった．かなり分かり易い．たとえば，A5は#3×10, #5×6で16この素群を持っているが，同型な部分群を除くと２個しかない．素群数をカウントしていない．⇒対処した．

◆群の検査で群が巡回群であるか否かを判定する．⇒素数位数の群は巡回群である．「自乗元とならない元が単位元を除き１個しかない群は巡回群である」と言えるかどうか？多分言えそうな気はする※．素数判定ルーチンを久留島喜内から持ってこなくてはならない．喜内では複数の素数判定ルーチンを持っている．IsPrimeはTotientFuncを使っている．FactoringSubでは因数分解を実行している．どちらも高速化するためにかなり技巧的なことをやっている．⇒こちらではそれほど大きな数を扱っていないので，簡単なルーチンで済ませることにしよう．

※位数3のA3は反例である．{e, 1, 2}のとき，1^2=2, 2^2=1で2乗元を持たない元の個数=0だが，この群は素数位数なので巡回群だ．逆にscount=0なら巡回群と言えるだろうか？この項目はちょっと保留ということにしておく．⇒巡回群の定義に従って修正した．

https://qiita.com/asksaito/items/76b71602dd956b79dbf7

▲S4の部分群分解を実行して部分群検定で停止した． (Count != 部分群数)になっている．Count = 28, 部分群数=29．おかしい．再現しなくなってしまった．⇒いや，再現できる．極小部分群の戻り値を部分群数から素群数に変えたためだ．素群数には単位群が含まれていないためだ．部分群数には単位群が含まれている．

◆DataGridViewに乗積表を出すことにしよう．乗積表が別に出せるようになると，コンソールもすっきりして見易く・使い易くなる．⇒久留島喜内のForm2を丸ごと移せば，ほとんどの機能がそのまま使える可能性があるので，コード変換を試みた．ネット上にも変換ツールは転がっているが，Code Converterというプラグインがあるので，インストールしてみた．かなりのエラーが発生する．コード部のエラーは手直しが効くが，デザイナー部のエラーは修復が難しい．どうせやるのなら，久留島喜内を丸ごとC#に移植した方が分かり易い．

ただし，これはかなりの大仕事になる．前回のELSIEですでにVB→C#変換というのは経験しているが，ELSIEはコンソールアプリなので修復も大した手間が掛からなかったが，道具箱はツールが満載のフォームなので作り直すしかないかもしれない．VBはもうじき廃盤になるという話もあるので，C#に移行しておくというのは正しい選択ではないか？

準同型検定というのは予想より難しい．これは後から考えるとしてまず，同型検定から片付けよう．wikiには「共役部分群は同型であるが、同型な部分群が共役であるとは限らない。」という記述がある．これは同型⊂共役という我々の観察と一致しないのではないか？以下のリンクでは，A5の位数6の部分群は互いに共役だが，異なる３つの同型類に分割されるとしている．

https://www.facebook.com/groups/2354748741306929/posts/6802031046578654/?comment_id=6805344309580661&reply_comment_id=6806265776155181&mibextid=zDhOQc

wikiには「アーベル群は同型な 2 つの異なる部分群をもつかもしれないが、それらは決して共役でない。一方でシロー部分群は互いに共役である」のようにある．可換群はあまり登場しないが，Vは位数4のアーベル群で３つの位数3の部分群を持っている（これらはすべて正規部分群）ので，試してみることにしよう．⇒すべて共役となってしまった．共役と同型は包含関係ではない（交叉する場合はある）とすれば問題は解消するが，いまのところ同型で非共役という事例は見つかっていない．

◆共役関係で台集合を同値類に分割するということをやってみる．

◆群の検査では群の情報をできるだけ表示する．たとえば，群の置換表示，正規部分群，極大部分群など．共役な部分群の表示，親群

▲button5_ClickでConsole.WriteLine(“\n同型判定：{0}”, testname);の中でハングしてしまう．⇒Console.WriteLine(“\n同型判定：”+testname);の形式に書換えたら動作するようになった．

https://mathlandscape.com/normal-subgroup/

n↦gng^−1のような変換を「共役変換」や「相似変換」や「内部自己同型」と言ったりする．正規部分群とは共役変換しても不変な部分群である．つまり，gNg^-1=N．

同型判定は大体動作している．たとえば，S3の正規部分群S3:<3>とA3が同型であることが判定できる．

▲「置換リストを使わない」というオプションで例外が発生した．対象はA4で部分群検定の初期化→部分集合[0] = new string[] { e };でエラーが起きている．Nが０になっている．A4を使うためには，まず置換群の生成で群が生成されなくてはならないが，その前にS4の置換を生成することが必要だ．どうも置換の生成で失敗しているようだ．置換リストを使わないというオプションでも生成できなくてはならないのだが…

Permutation.Createが動作していない．⇒置換群は通常のやり方で生成し，群同型判定のときだけ「置換リストを使わない」ように切り替えることで一応動作するようになった．しかし，いずれにしても，位数の異なる群の準同型写像は確立されていないので，検定にはなっていない．⇒いや，位数が異なる場合にも対処しているはずだが，台集合が書換えられていないように思われる．⇒いや，すべての置換を試している．一応検定にはなっていると思う．いや，やはりおかしいような気がする．L1とL2の長さが異なるということは写像になっていないのではないか？

長さが同じでもすべての置換を試してみるしかない．長さが異なるときにはさらに膨大な組み合わせが発生する．この検定では位数が同じ場合に限定するしかない．マップは冗長構成になっているので，実長が一致しない場合は棄却するしかないと思う．写像クラスはそのような前提で作られていると思われる．実際，ｎという値はmap1と2で共有されている．⇒群同型判定は(A.N != B.N)で抜けるようにした（復活）．

まだ，おかしなところがある．A3とA4:<b>は同型になるが，L1の長さが6もあるのはなぜか？Aの台集合に{a, b, c, d, e, f}が入っている．かなりおかしい．A3の台集合が間違っている．A3は外部で生成されているだけなので，設定に誤りがあるのではないか？いや，A3は元々位数6の群だから台集合は間違っていない☓．Nがおかしい．置換群の生成でやり損なっているのでは？確かにそのようだ．かなりまずい．どうも，置換の個数と位数を混同している気配がある．A3の置換は置換数3でよいはずだ．S3の置換が6でその半分だから3になるはずなのだが… いや，置換はm=3, n=3だから合っている．間違っているのは台集合だ．

▲S5の位数と台集合サイズが一致していない．m=120に対し，台集合は121になっている．一つ多過ぎる．⇒修正した．

◆部分群リストに追加：で位数を表示する　⇒対処した．本ツールでは位数を#xxの形式で表示している．orderと#(No.)は親近性がある．

位数が等しくない場合には準同型検定ができないとすれば，同型検定と結果は同じになる．準同型検定は不要なのではないか？準同型検定ではすべての置換を生成して準同型写像を探している．それが不要になるというのは結構なことだが，果たして同型検定だけで十分なのかどうかまだ見極めが付いていない．同型検定の中では準同型判定を使っているのだが，どのような写像でも同型になるとは限らないと思われるのだが… いましばらく，このままで検定を続けることにする．かなりいろいろなことができるようになってきた．

A5の位数6の部分群をチェックしてみた．どうもこれらは同型であるような感じだ．同型判定では非同型となるが，準同型判定では準同型写像を見つけている．同型であるものを非同型と結論することはできないから，準同型検定を廃止するのではなく，むしろ同型検定に準同型検定を持ち込むしかない．同型検定は簡易検査として論理を残しておいて，非同型となったときだけ準同型検定を実施すればよい．これによって，準同型検定は正式に廃止できるが，まぁ，当面形だけは残しておこう．

同型検定まではこなせるようになった！まだあちこち未整備のところがあるので，きれいにしてから共役に移ることにする．