今日はこれまでで一番冷え込みがきつい.特別給付金が振り込まれたら灯油を追加購入しようと思っているのだが,市役所からは何の応答もない.ポットも壊れてしまったので,炊飯器を茶釜代わりに使っている.まぁ,これもそれなりに「優雅」な気がしないでもないが…


それよりも,床が沈んで冷蔵庫が傾いている方が問題だ.わたし自身が,身体的に傾きかけていることの象徴のように見える.もう,終わりも近いのかな?つまり,いよいよ末期に突入ということだろうか?
コラッツ高速道路系はプログラム的にはほぼ完成し,マニュアルを書くだけという段階に達しているが,ここに来て,「完全正則コラッツ木を構成するためのもう一つの方法」というのが見つかってしまったため,急遽方向転換を図る必要性が出てきた.もう一つの方法というのは至って単純なもので「3の倍数ノードを一律除去する」というだけだ.コラッツ核木ないしコラッツ長子木と呼ばれるこれまでの方式は,あるノードの子ノード,つまり兄弟ノードを一括して長子ノードに代表させるという方法だが,この方法にはいくつか問題点がある.
一つは,1と5が直結しているため,この状態では完全正則木とは呼べないという点がある.これはある意味で1と5という2つの整数の特殊関係を示すものとも考えられるので,一概に退けるべきものではないが,完全正則木として扱うためには5をルートとしなくてはならないということを一々説明しなくてはならないというのもかなり厄介な話だ.
梶井基次郎の「櫻の樹の下には」ではないが,コラッツ木の根本には小さな有向サイクルが埋まっている.つまり,(1, 2, 4)という有向閉路だ.これはコラッツ予想問題の鍵とも言うべき急所だが,1ではなく5をルートとして議論を進めるというのはあまりわかり易いストーリィではない.(1は地中に埋まっていると言って納得する人はいるだろうか?)また,本来なら行き止まりであるはずの3の倍数ノードが処々に出現するというのも分かりづらい点かもしれない.また,この構成では素数の一部が完全正則木に含まれないという状況も発生する.これらの難点は,3の倍数を正則木から除去することで一挙に解決する.
この意味では明らかに後者の方式に分があるように思われる.実際,以前コラッツバスケット上で問題を考えていたときにも,3の倍数を除外するというスキームを試みたことがある.このときは,それによっても問題がほとんど易しくならないので一旦は放棄されたコースではあるが,むしろこちらこそ本線なのではないだろうか?
コラッツ銀河高速道路系には,一般道路と高速道路という2つの系統の区分があり,その「相互乗り入れ」つまり,インターチェンジというのが計算上の難所になっていた.このような問題はすでに全面解決しているのだが,それらの成果をすべて捨ててまた振り出しに戻るというのもかなりきついものがある.しかし,シンプルイズベストというオッカムの剃刀の原理に従うとすれば,選択の余地はない.
ここで方向転換すると「コラッツ銀河高速銀河系」はまったく使われないことになる.なぜなら,3の倍数ノードを除去したコラッツ木には一般道路と高速路という区別は存在しないからだ.しかし,せっかくここまで練り上げたものをただ捨てるというのももったいないので,ともかく,完全に仕上げてからお蔵入りさせるということにしたい.というか,すでにその水準に達していると思われるので,いまここで「コラッツ銀河高速道路系」を恒久的に凍結するというのでよいのではないか?これまで使ってきた「仮想木」という概念も破棄されることになる.
銀河高速道路系というイメージを放棄するとしたら,3倍数を除去したコラッツ木のイメージをなんと表現すればよいだろう?この道路網の特徴は中心点から全方向に放射状に道路が伸びているという点にあるので,コラッツ放射線道路システムとでも言うことになるのではないか?この道路網の特徴はノードを水平に接続する環状線がまったく存在しないという点にある.つまり,合流点以外の交差点は存在しないという道路網だ.英訳すれば,Roads radiating in all directionであり,Radial Roads と呼ぶこともできる.

このイメージを採用するとすれば,プロジェクト名はコラッツ放射線道路系,Collatz Radial Roads Systemということになる.ちょっと膨らみのない名前になってしまうが,もっと直截に表現するとすれば,Collatz Complete Regular Treeということになるので,これまで使ってきたCollatz Tree GeneratorをCollatz Complete Tree Generatorとすればよいのではないだろうか?少し長くなるが,これが状況を一番よく表現しているような気がする.あるいは,Collataz Complete Treeでもよいかもしれない.これが一番わかり易いのではないか?
Collatz Complete Treeというのは正しいネーミングであると思われるが,むしろ,これまで使ってきた,Core Treeという方が直感的かもしれない.Complete Treeというと,正則であることを説明し,それが完全正則であることを付け加えなくてはならないが,Core Treeと呼べば必要かつ最小限の核に該当するということは理解され易いのではないか?従って,製品名はCollratz Core Tree つまり,コラッツ中核木ということになる.これでゆくことにしよう.
ゼルコバの木の開発用フォルダが5GBを超えている.本来このプロジェクトは高々2MBくらいだったと思われるので※,5GBもあるというのは異常だ.この原因は.vsというフォルダにある.このフォルダ一つだけで5GBを超えている.このフォルダはテキスト入力補完のための使用頻度の高い語句を収納した一種の辞書のようなものだが,このようなものがプロジェクトフォルダの内部にあるというのは問題だ.以前は外部に置いていたような気がするのだが…しかし,どこで調整すればよいのだろう?⇒方法が見つかった.
※2MBというのはさすがに過小評価だ.ゼルコバの木アルファ版のころはそのくらいだったかもしれないが,現在は開発用フォルダ全体で730MBくらいはある.
https://stackoverflow.com/questions/19398287/ipch-files-on-a-visual-studio-project/41138541
ツール→オプション→テキストエディタ→C/C++→詳細設定→フォールバック位置で「つねにフォールバック位置を使用」をオンにすると,システムの固定の場所を使うようになる..vsフォルダをまるごと削除してみよう.ソリューションを開くとこのフォルダは再生してしまうが,ipchフォルダは消えて,以下のようなメッセージが表示される.
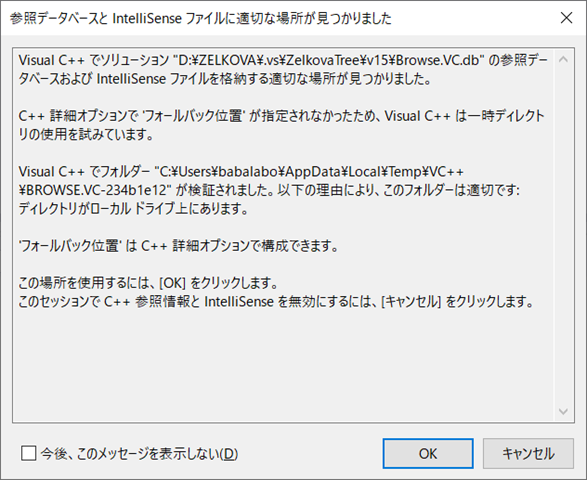
上記のフォルダに既存のipchフォルダをコピーしてやろう.⇒うまくいったようだ.これで個別フォルダに入っているipchは不用になったので,削除しておこう.1個が5GBもあるので相当な量になる.⇒いや,こういう状態になったのはつい最近,つまりOSを再インストールしてからのようだ.それまでは「適切な場所」に保管されていたようだ.
画面レイアウトは基本的に従来通りだが,ラベルの付け替えを行った.
- Virtual tree → Core tree
- Degree → Max-branches
- Get branch position → Branch Location
- Verify → Verification test
- Get the sequence → Get Collatz sequence
- Get the number → Address to number
- Enter a branch order sequence separated by comma → separated by period
グラフ理論で一般的に定義されているdegreeと我々の用語の食い違いを調整するため,Degreeという名称を廃止してBranchに統一した.Sequenceという用語はコラッツ数列と枝番号列として使われているが,枝番号列はBranch Locationを指定するためのアドレスとして用いるということを明確にするために,Get the numberはAddress to numberに変更した.Branchという語は支店という意味で使われるのでBranch locationというと「支店所在地」のような意味になってしまうが,このコンテキストでは「木の枝」を扱っていることは明白なので多分誤解を招くことはないのではないかと思う.
コラッツ数列というのは,13→40→20→10→5→16→8→4→2→1のような「コラッツ写像」から導かれる数列で,コラッツ予想問題をやっている人には一番わかり易い表現ではないかと思う.コラッツ数列→コラッツ木アドレス→奇数→コラッツ数列の変換がもっとも重要なポイントであり,そこの点を飲み込んでもらう必要がある.
ゼルコバの木を改造して隣接リストをインポートできるようになれば,外部出力は隣接リストだけで済むことになるので,まずそれを決めてしまうことにする.コラッツ問題を解析する上でゼルコバの木の重要性は増しているので,コラッツ中核木生成ツールのリリースと前後してゼルコバの木コラッツ特注版をリリースすることに決めた.
コラッツ木はもっともシンプルな系図木であり,この図面が描画できないようでは話にならないというところから考えても,一度原点に戻って論理を洗い直す必要があると考えている.既存ゼルコバの木は高度な機能/パフォーマンスを求めるあまり,やや偏極する方向に逸れてきたのではないかと思う.このバイアス(歪曲)を戻してオーソドックスに戻る必要がある.このためには,まず,このコラッツ特注版が安定かつ高速に動作するところから始めなくてはならない.
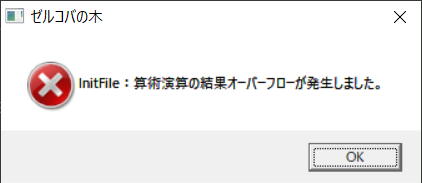
現行ゼルコバの木のメニューでは「一覧表のインポート」でCSVファイルを読み込んでいるが,隣接リストは一覧表データではないので,独立のメニューコマンドとして「隣接リストのインポート」を追加することにする.⇒大体できた.いい感じだ.ファイルをインポートしたときには,デフォルトで画面に合わせてズームで開くようにした.実用的に使えるようにするためには,①テーマの登録と選択,②部分図登録の部分がきちんと動くようにしておく必要がある.現行では標準画面設定は枠線なしになっているが,枠線ありで最小幅とした方がよい.⇒登録しようとしたら,エラーが発生して異常終了してしまった.「パスへのアクセスは拒否されました」となっている.
IO.File.Move(selectname, newname)というコマンドを実行しようとして拒否されている.このコマンドはファイルの移動ないしリネームを実行するためのものだ.オリジナルファイルを退避させる目的で実施されているものと思われる.フォルダは一部読み取り専用になっていたので,解除してみたが動作は変わらない.エクスプローラで手動で変更することはできる.プログラムからの変更はできないようになっているのだろうか?このファイルはProgram Files (x86)/Common Filesに入っているので,アクセス制限が掛かっている可能性はある.⇒ファイルの所有者がTrustedInstallerになっている.これはかなり厄介だ.いつからこんなことになったのだろう?
設定ファイル類をここに置いているのは,ドキュメントなどに置くとそのユーザしかアクセスできなくなることを避けるためだったのだが…そうしないと,インストール時のオプションで「誰でも使える」とする意味がなくなってしまう.⇒VSを管理者モードで起動すれば変更できる.多分一般ユーザも管理者としてログインしていればプログラムから変更できるのではないかと思う.これは確認する必要があるが…
▲画面設定を変更して保存→終了しようとして,PAGESETUP::GetPageCountで停止した.(treeview()->validcard && !NearZero(wholeH % GH))という状態になっている.全体高=1005でGH=190から,1005/190=5…55となり,余りが出てしまっているためだ.この理由は後日調べるということにしておく.⇒上記で再登録した標準設定は動作しているようだ.
▲TruncatedTree 14を206307でソートしようとしてGetGenerationで停止した.(_generation < 0 && !showUnderWear)で_generationの値が-4になっている.絶対座標系では世代番号は負にはならないことになっているのだが…かなり始末が悪い.シューティングが必要だ.