ゼルコバの木テント村
階乗の末尾連続ゼロ数は基数のｂによって決まる．ｂの素因数分解に含まれる素数をｐとするとき，N=n!に含まれる最小のｐ^eの個数が連続ゼロ数となるので，最小のｐ^eの個数を決定する必要がある．一般にはpが大きいほどこの値は小さくなるが，pが小さくてもeが大きければ逆転する可能性がある．
まず，一般的にｎとｂを指定したときの連続ゼロ数を与える関数を作ってみよう．このためには，ｎを素因数分解するところから始めなくてはならない．julia には factor という関数がある．以下のダンプは b=2^2・3 を表している．
b=12 f =Primes.Factorization(2 => 2, 3 => 1)
Factorization というのは連想配列で，とりあえず，
for (p, e) in f
@printf(“%d %d \n”, p, e)
end
の形で取り出すことができる．
Julia がさっぱり動いてくれない．わたしのボケが進んでいるためかと思ったが，Julia の使いづらさ（不備）というのもあるような気がする．ブレークポイントが聞く既存プロジェクトに対象となるコードを埋め込んでみたが，ブレークしない．既存コードでも同じようなことが起こっているが，plot を呼び出さなければブレークできるところを見ると，どうも，デバッガが動くコードと動かないコードがあるように思われる．停止点がそのコードより前にあっても停止しないので，おそらく実行時に先読みしているのだろう．
確かにplotが動作するようになるまでかなり手間取った記憶はある．plot というのはウィンドウを開いてグラフなどを表示するための関数だが，何も出てこないということはまるきり動作していないということだろう．多分，どこかに plot が動くバージョンは残っているはずだが，どうやって動かしたのか忘れてしまった．現在仕掛りのコードでは，おそらくPrimes というパッケージがそれに該当するのだろう．いや，Primes はコメントアウトしてある．
ファイルは新規生成しただけでは実行されない．外部から持ち込んだだけの場合も同様．「保存」が必須のようだ．
ひさびさにJuliaを起こしてみたが，使い方をすっかり忘れてしまった！functionの書き方どころか，コメントの付け方さえ忘れている．二重階乗というプロジェクトがあったので，コピーしてここから始めることにしたのだが… 環境も変わってしまっているような感じだ．using Primes が通らないので，再インストールしている．Julia は間に GitHub が入っているのでいまいち何がどうなっているのかよく分からない．というか，その前に Juliaの拡張が入っていない．というか，２，３日前に Windows 11 をインストールしているのだが，それが裏目に出なければよいのだが… エクスプローラの詳細表示で行間が広くなっている．こういう変化はうれしくない．
GeoGebraのIF文がどうやっても通らない．こんなつまらないところで躓くとは… 何かシンプルなサンプルはないだろうか？
▲q1とp1の交点T2(C_1)は辺CA上に乗っていない．わずかながらずれている．作図ミスと思われる．q1とp1はいずれも円だ．q1(l2, V), p1(T1, V)．Vは円周上の点でV(c1, j)だが，これが間違っているのではないか？jは(L, C)という直線でLは直線i上の点だ．i(A, B)でこれは間違いようがない．どうもLは点Aを選択したつもりで新たな点として追加されたものと思われる．⇒これで正しく動作するようになった．Point(…)を総点検する必要がある．Lは削除しておこう．
周長２等分線図の包絡線図を出せるようになった．できれば，この表示を切り替えるできるようにしたいのだが… オブジェクトの表示・非表示を切り替えるボタンを設置できるようになっている．チェックボックスにはオブジェクト・リストを選択できるようになっているので同時に切り替えが可能だ．ただし，オブジェクトの属性をここで切り替えることはできないので，直線を２種類作らなくてはならない．⇒それはそれでよいのではないか？しかし，このスイッチは表示・非表示を切り替えるだけなので，AとA’を切り替えることはできない…
リストを作るときにはオブジェクトを矩形で囲んで選択する．これは編集できるので，なんとかなりそうだ．ボタンを設置してスクリプトを書くという手も考えられる．オブジェクトの表示・非表示と属性（色と線の太さ）を変えたいのだが… 切断線は３本のはずなので，個別に書き換えてもそれほどの手間にはならないのではないか？
GeoGebraには軌跡の方程式を求める機能が備わっている！「数式処理 (CAS) エンジンでグレブナー基底を用いた計算を行い，軌跡の方程式を求めている」という．なんてこった！⇒ただし，求められるのは点の軌跡だけのようだ．つまり，直線の方程式を求めることはできない．まぁ，点の軌跡を得られればそれから割り出すことは可能だろう．
駆動点はなんらかの動線上の点でなくてはならない．P点をある円周上の点に設定し直すことはできるのではないか？その上で，小三角形上の点の軌跡の方程式を求めれば，その点とPを結ぶ直線の式は導き出せるはずだ．ただし，GeoGebraでは文字式は使えないので，方程式の係数はすべて数値になっているはずだ．それでも，方程式の形式がわかるだけでも有用性はあるだろう．⇒どうだろう？役に立つ場合もあるかもしれないが，あまり役には立たない気もする．
得られるのは軌跡の（駆動点とは独立の）方程式であり，駆動点との関係は捨象されてしまっている．このような式が与えられたとしても，それをどう利用すればよいのか？にわかには思いつかない．以下の記事ではGeoGebraを高校数学の授業に活用することを念頭に動作確認しているが，この機能にはまだまだかなりの限界があることが示されている．
https://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1951-15.pdf
久留島喜内の道具箱は結構作り込んであるつもりなのだが，まだまだだ．このツールは本来べき乗剰余の周期列を見るためのものだが，対象数の逆数をB進数表記で見ることもできるようになっている．べき乗と逆数には強い関連があるためだ．しかし，ときには対象数の逆というより，除数を分母としてみたい場合もある．そのような見地からすれば，現在の動作はγ＝１の場合を見ているに過ぎない．
また，現状ではB進数表記にもかなり制約があるように思われる．対象数が大きくなると簡単に表示不能になってしまう．もっと桁数の大きい数値を扱えるようにする必要がある．1/αの表示形式にもやや問題がある．間仕切りの｜は却って邪魔になっているような気がする※．仕様も使い方も忘れてしまったところがあり，stripeなどの意味もわからない．せめてヒントくらい出るようになっていないと… いや，ほとんど忘れてしまっていると言っても言い過ぎではない．マトリックスが２種出るようになっているが，なぜ２つも出しているのかも忘れてしまった．
※本家AMSツイッタの常連投稿者の pink @fourtyonerocks が4/13 = 0.(307692)という書き方をしている．これは読み易いような気がする．
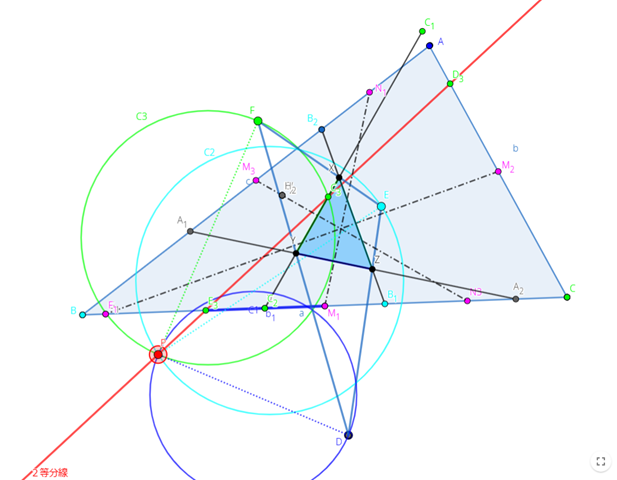
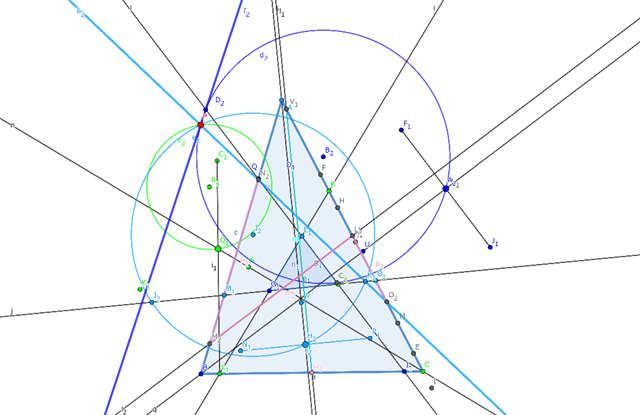
前日のログで，「動作のおかしいところがある」としているが，やはりおかしいと思う．これらの点は⊿XYZの辺の延長と⊿ABCの辺の延長の交点だが，飛び出す点と飛び出さない点がある．飛び出さない点は上図にコーナーを回って隣の辺に移動している．この動作の方が正しいと思う．いや，それでは定義に反するものになるのではないか？たとえば，C1とC2はC点から等距離でなくてはならないはずだ．むしろそうなっていないA2の方が間違っている．A2はIntersect(L1, t1)となっているが，t1というのは⊿ABCそのものだ．
L1は線分ではなく，jとbの交点だ．いや，L1という点とL1という直線があるのではないか？L1というのはC点の別名のようだ．しかし，この修正はかなり難しい．１点を修正するとその副作用で複数の点が未定義になってしまう．A1, A2というラベルの付いている点は表示用で，オリジナルの点は直線上の点になっている．A1, A2のラベルの付いている点を非表示にして，オリジナルの点を表示するようにした．多分これで動くはずだ．⇒すべてのオブジェクトを表示設定して修正した．
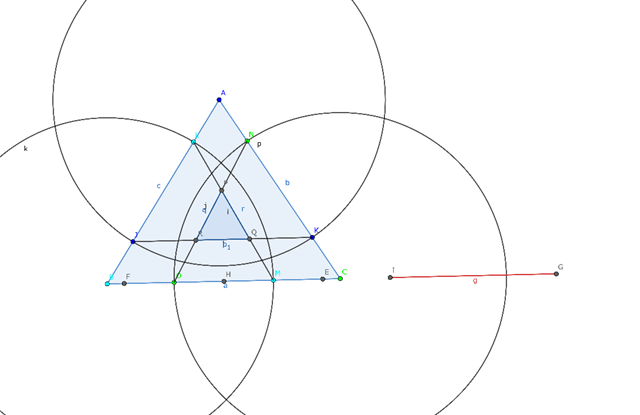
三角形の周長２等分線図（包絡線）を GeoGebra に投稿した
https://www.geogebra.org/m/xa7nsrpg
動作のおかしいところがある．
Aの左にグリーンの◯が飛び出している．いや，これはノーマルなのかもしれない．辺ACは短いので周長/4の点が延長に出てしまうのだろう．まぁ，これは現在の仕様では仕方ないのかも知れない．２個の点を線分で結んでおけばよいのではないか？
周長２等分線図（全域版）をXに投稿した．これを見たのかどうかは分からないが，おしろい(Face Powder)とOmolesho Quadry Abiodunがフォローしてくれた．これでフォロワーが４人になった．
結構いい線まで行っているのだが，てこずっている．要領は大体分かったので，作り込んでゆけばよいはずだ．目標は，P点を全領域で動かせるようになることだ．つまり，P点がデカルト平面上のどこにあっても，与えられた三角形の周長等分線が引けるというのがゴールだ．P点が三角形の内部にあるときは，場合によっては等分線が２本になる場合もある．このような場合にも正しく動作するようにしなくてはならない．図面に書き込んでいる円の個数は１８個，多分これ以上増えることはないと思われるが，直線ないし線分の数はその何倍もあり，それをまた上回る数の点がある．おそらく，最終的にはオブジェクトの総数は数百個に達するのではないかという気がする…
この図面にはおそらく６個の象限があると推定されるが，現在のところそのうちの2.5象限しかカバーできていない．まだ未整備のところが多々あるためと考えられる．それらを潰してゆくしかないだろう．blueの領域がまったく出ていないのはなぜだろう．すでにF点は決めてあるのだが，N点が定まっていない．まず，ここから片付けることにしよう．F点というのは頂角の２等分線上の点でこの点とPの中点を中心とする円がN点の位置を決定することになっている．N点はL2上の点であり，L2というのは，３本の基線のうちの一つだ．
大体全域で動くようになった．ただし，まだ問題点がいくつかある．内部の三角形と小円が交差するとき，２点で爻わる場合，どちらを取るかという問題だ．どちらかを消さなくてはならないが，それを図形から判断できるだろうか？スクリプトを使って切り替えることができれば話は簡単なのだが… 実際，現在の実装では目視で明らかに２等分になっていない場合がある．⇒１本線を消したら正しく動作するようになった．⇒等分線が３本出てくる場合がある．この動作は正しい．
ナムの三角形周長２等分線作図問題の一般解をGeoGebraで書こうとしているのだが，なかなか難しい．できるだけ画面をすっきりさせたいのだが，余分なゴミが出てきてしまう．これはポイントが落ちてしまっているためだろう．たとえば，下図には３本千切れた尻尾出ている．
これの固着できない点はどこかの線分の延長上にあったのではないだろうか？⇒単純に消しておくだけでよいのではないか？どうも，そもそも仕様通りの動作になっていない．実装が悪いのか，設計が間違っているのか？もう一度作り直しするしかない．
真ん中の小さい三角形は包絡線図でかなり重要な図形になってくるが，⊿ABCの形状によっては描画できないことがある．線分との交点ではなく，延長上の交点を取ってみる．
