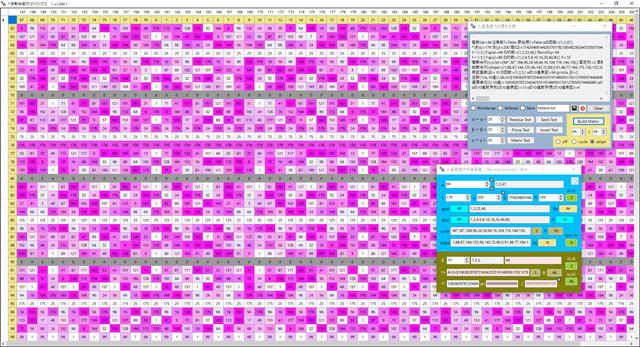
Lambda関数で直接周期桁数と固定桁数を返せるようにしたいのだが,頓挫している.どうすればよいか?やはり,1点づつ検査するしかないのではないだろうか?桁数は判明しているのだから,それを使ってやりくりすればなんとかなるような気がする.修正を試みているところだが,反例が出た.offset=0 <> drop=2 α=6 γ=18 Λ=0.この事例では数列は{6*, 0*}で2#0だ.⇒これは通ったが,別の反例が出てきた.offset=2 <> drop=0 α=7 γ=18 Λ=3.この事例では数列は{7, 13, 1}で0#3,また,反例が出た.offset=0 <> drop=2 α=12 γ=18 Λ=0.このサンプルは{12*, 0*}で2#0だ.まだダメだ.offset=0 <> drop=1 α=15 γ=18 Λ=1.このサンプルは{15*, 9}で1#1だ.⇒どうやらできたようだ!これができると,今度はΛとオフセットを使って剰余周期列を生成できる.⇒既存のGetResidueCycleは廃止し,別途MakeResidueCycleとして作り直すことにする.
いや,オフセットと周期が分かれば,具体的に数列を与えなくても色分けはできるはずだ.次のような手順になる.
- mat.RowTopからmat.maxrows分以下を行う
- 先頭列が固定部(オフセット)の範囲内ならば,テーブルの行を走査して初項を見つける.初項が見つかった位置から塗りつぶしを開始する.
- 先頭列が固定部(オフセット)の範囲外のときは,すでに区間に入っているものとして,塗りつぶしを開始する.
- 塗りつぶし中にゼロ項を検出したときは,そこで打ち切り
- 塗りつぶし中に1項を見つけときにはそこで塗りつぶしを中断し,ステップ5に戻る.
一応動き始めたが,まばらなところがある.
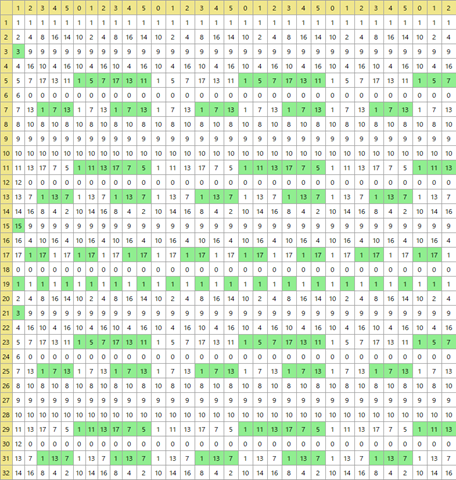
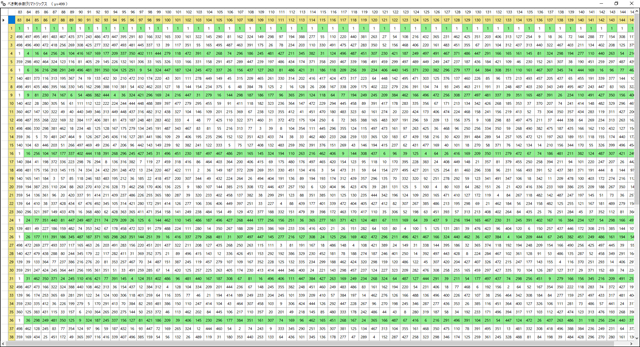
1の入っている周期列は大体表示されているようだが,それ以外は全滅だ.初項が見つかっていないのではないだろうか?⇒Lambda関数が悪い.α=1,γ=1で0を返している.⇒ようやくできたようだ!予想外のかなり興味深い図柄になった.

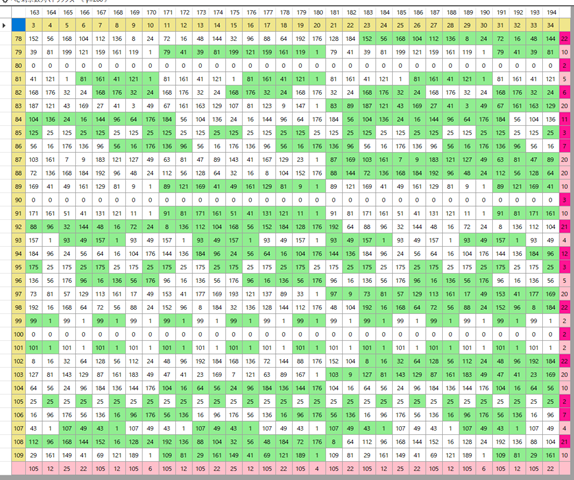
図で見ると垂直方向にも周期性がある(かの)ようにも見える.もう少し拡大した図を出してみよう.

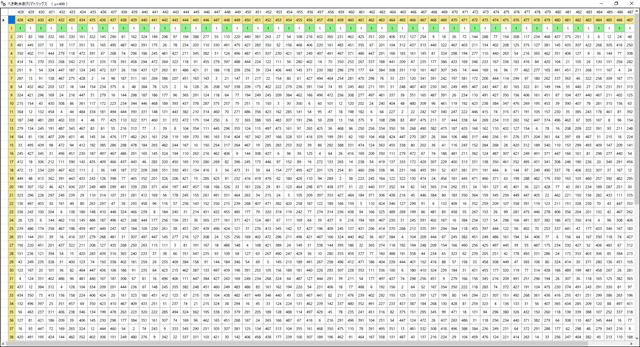
縦数列の周期性がはっきり見える.γ=18を3分割して3種のパターンが繰り返されている.このパターンを反転させるとどう見えるか?というのも興味深いところだ.上の図にはまだ誤りがある.6, 12, 24, 30などで頭の固定部が塗りつぶされている.それを修正すると,上記パターンの反転は完全に同型になるはずだ.試みに反転パターンも出してみた.

パターンは完全に同型だが,左右反転したものになっている.個別の行は固有の反復周期を持っているが,全体としてみると,それらの公倍数となる反復周期が観察される.いまの場合の全体周期は12だ.この12という数はおそらくφ(γ)の約数列から出てくるものであろう.
さて,どこまでできているのか見てみよう.⇒ダメだ.かなり崩れている.γ=100で試してみたところ,大体は合っているが,間違っているところが出てくる.設定はα=15,ε=115となっているので,Rα=15とRε=35が画面中央付近に配置されるようなマトリックスになっているが,どうも,取っ掛かりのところで失敗しているようだ.後ろの方を見ると正しい周期に乗っている.
たとえば,α=6の剰余数列は,{6*,36,16,96,76,56,}で1#5となっているので,頭項が36,末項が56でなくてはならないが,6で始まって76で終わっている.その次からは頭項36で周期に復帰している.そもそも6は固定部に含まれるので除外されなくてはならないのだが… 結局,offsetを持つ剰余数列をうまく処理できていないと見ることができる.⇒できたようだ.⇒と思ったのも束の間,α=100,ε=115, γ=200で真っ白になってしまった.どうも,αが64を超えると誤動作が始まるようだ.65ではまだある程度まではカラー表示されているが,70ではまったく表示されなくなる.⇒大体動作するようになった.
εを操作して,枠外にはみ出すように調整しても,マトリックスがその位置を含むように開かれない.1~64の部分が表示されたままだ.α-100, γ=200, ε=79で,Rαは100,Rεは79だが,Rε=79は圏外だ.つまり,マトリックスを生成する論理ではマトリックスの水平シフトがまったく実施されていない.⇒ある程度安定した動作になってきているので,一度バックアップを取っておこう.
mat.ColumnTopはBuildMatrixで決めている.多分この論理が間違っているのだろう.Rε > maxcolumsの場合,ColumnTop = Rε – maxcolums \ 2という値が入っているが,ColumnTop + maxcolums >= maxの場合にはColumnTop = maxcolums + 1に修正されている.⇒この補正を止めたら動作するようになった.この補正は何のために入っているのか?max=γであり,このテーブルのサイズを意味している.γがMAXSQUARESIZEを超えている場合には物理的にテーブルを構成できないので縮小する必要があるためのパラメータだ.
maxcolumsはマトリックスの横幅であり,ColumnTop + maxcolumsというのは,マトリックスの右端を意味する.これはおそらく,マトリックスの右端がMAXSQUARESIZEを超えないための措置と思われるが,誤った論理になっている.書き直しておこう.これで横数列の周期カラー表示は大体まとまったのではないかと思う.

あと,これに縦数列の周期カラー表示を追加すればほぼ完成になるのだが,こちらの方は横数列ほど単純ではない.横数列の周期カラー表示を見ても分かるように,縦数列にも周期性が認められることは確かだが,縦数列の難しいところは,①回文というパターンがある,②一つの周期の中で同じ文字が複数回出現する,などなど.この周期性を確定するのはかなり難しい.しかし,縦数列の長周期はγに固定されているので,周期性があるとすれば,γの約数でなくてはならないから,ある程度までは絞り込むことができる.もちろん,γが素数なら周期は存在しない.
横数列で0の並びになる場合がある.このような行が存在する場合には,その行を区切りにした周期が発生する可能性がある.たとえば,γ=18の場合,6^2≡6^3≡0 mod 18dだから,周期6の数列ができる{1, 8, 9. 10, 17, 0}や{1, 10, 9, 10, 1, 0}など.
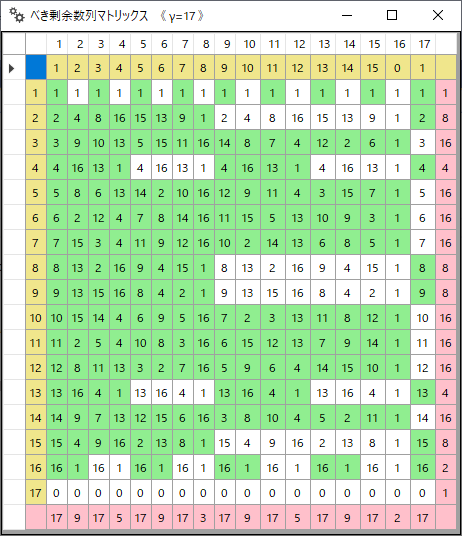
▲マトリックスの0行の表示がおかしい.γ=18のとき,{1, 2, 3, 4, 5, 0}の繰り返しになっている.γ-1=17の剰余になっていなくてはおかしい… 除数がΘ=φ(γ)になっている.いや,この表示は正しい.⇒やはり,異種文字数の表示は必要なのではないか?
▲このマトリックスにはまだ不備がある.列ヘッダに入っている番号が1からの通番になったまま変化しない.これでは問題がある.マトリックスの左端には固定部が固まっていて,これらは循環に関与しないため,Rεの値だけでは位置決めができない.たとえば,α=3, ε=121の場合,Rα=3,Rε=1の位置,つまりM(3, 121)には3という値が入っているが,Rは9である.同様のことは行についても言える.(ただし,行では実害はない)たとえば,α=123としても,行ヘッダの番号は変化しない.⇒αとεが生値でヘッダに現れるようにする必要がある.
大きい数を扱おうとするとセル幅が大きくなってしまうが仕方ないだろう.つまり,Rα,Rεをマトリックス中央に配置するのではなく,αとεの生値が中央に来るようにすべきだ.⇒いや,元々そのように作り込まれている.何か(操作的に)勘違いしていたのではないか?いや,確かに上記のような動作になる場合がある.何か調整が入っているのだろう.ColumnTopとRowTopはBuildMatrixで決めているので,そちらを見る必要がある.⇒修正した.ようやく,思ったような図になった.
縦数列で一番肝心なポイントは,γの区間がいくつに分割されるか?という点だ.横数列の場合には,この値はφ(γ)に一致する.γが素数ならγ-1だが,一般にはΛの倍数である.場合によっては,この値をΛと呼んでもよいのかもしれない.あるいは,もっと相応しい名前があるかもしれないが,いずれ,何か名前を付ける必要性が出てくるような気がする.
縦数列の場合はもっとはっきりしている.γの範囲を等分するゼロが並んだ行が発生するからだ.この分割数はγの約数であるから,γが素数の場合には1となる.いや,もしかして,これもφ(γ)なのではないだろうか?そう考えてよいような気がする.つまり,縦数列は(γ-1)/φ(γ)個の縞に分割されると考えてよい.ただし,この縞は横数列のように同じパターンの繰り返しではなく,個別に異なるものとなっている.つまり,マトリックス全体はたかだか,(γ-1)/φ(γ)個の小ブロック=タイルで埋め尽くされていると考えてよい.この小ブロックのサイズはφ(γ)xφ(γ)である.縦数列の周期をカラー表示するとしたら,この小ブロックを塗り分けることになるのではないだろうか?