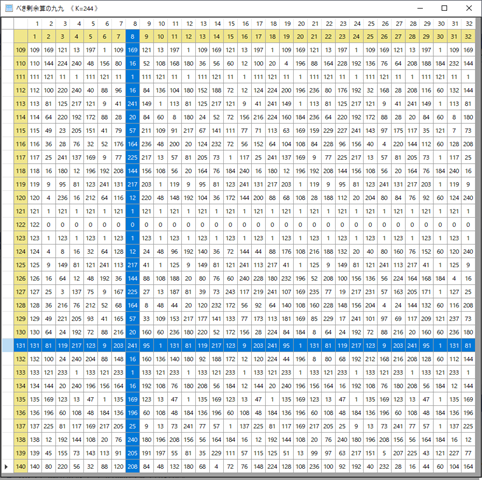
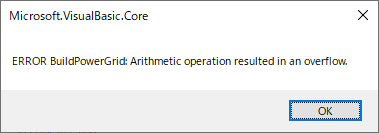
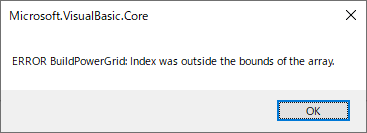
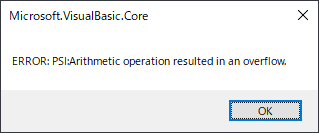
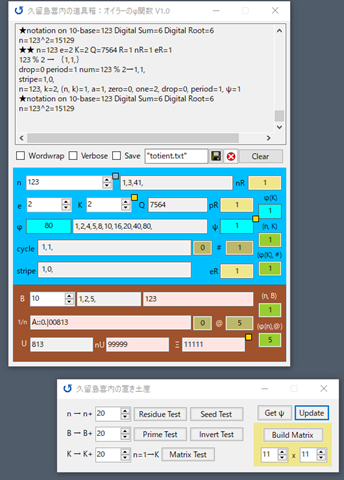
Getψ関数の仕様を再考する必要がある.ψ数はnとKによって決まるが,ψ数が決定できない場合もある.ψ数が得られる条件はNのべき剰余数列の中(終端)に1が現れることだが,剰余数列に1が入らない場合はいくらでもある.このようなときに,ψ数の定義に従って,nに対応したKの最小の値を決定するというのがGetψ関数の役割だが,その動作にはかなり疑問がある.①選ばれるKが極端に小さい.ほとんどは1, 2, 3, 5 のいずれかだ.②設定値ですでにψ数が確定しているのに,ボタンを押されるとより小さい値を探して提示するという動作になっている.
適合するKを1から探すのではなく,直近のK'<Kを求めるというのが適当ではないだろうか?逆に+Kの方を探すということも考えられるが,小さい方を探すというのが自然だろう.どのようなNに対しても,K=1, 2, 3, 5のいずれかは必ずψ値を与えると言えるだろうか?これは予想問題として立てておいてもよいかもしれない.
▲PsiFunctionはその中で表示出力している.⇒いや,Kの値を変えたときにValueChangedイベントが発生しているのだろう.⇒passflagを使って出力を抑制するようにした.
ψ数が求められる条件として「NとKが互いに素」というのが適用されている.これは正しいと言えるか?⇒EFAの定義表にもそう書いてあるので間違いないだろう.
▲N=10, K=1234567でハングしてしまった.⇒MakeStripePatternで手間取っている.文字列の長さを制限していないので無闇に長いテキストを生成しようとしている.⇒MaxOutput=10000で打ち切るようにした.⇒動作するようになった.
ψ(n, K)という関数は元々循環小数に関する議論の中で提案されたものであり,そこではu-length functionと呼ばれている.u-lengthとはnの循環節の長さであり,@と表記されている値である.従って,EFAの記述が正しいとすれば,u-length=ψ(n,B)で計算できなくてはならない.n=123, B=10のとき,@=5でnU=99999となる.このとき, N=10, K=123で剰余数列を計算すると#=5となって@の値と一致する.ただし,ψ値は不定のままだ.
n*U(b,n) = r*(by(b,n)-1)のような関係式が提示されている.U(b,n)は「循環単位」と呼ばれる整数値で現行ツールのUと一致する.上式の左辺はnUと呼んでいるものに他ならないから,この値が右辺式のように分解できるかどうかを確かめなくてはならない.
▲Nの入力値がMAX_INT64を超えているとき,黙って元の値に戻している.⇒パーツが上限を超える値を拒否しているためではないか?
EFAに記載された事例を検討してみよう.
… given n=21, you easily find out the remainder sequence {1,10,16,13,4,19,1,..}, while u-length function y(10,21)=6, U(10,21)=47619 and r=1. However if you take U=47619*x and r=x, then the equation holds for any x.
n=21, B=10とすると,U=47619, nU=999999 で @=6.r=1 であるかどうかは画面では分からない.⇒ nB=n%B という値も表示されてよいかもしれない.多分 r=n%Bのはずだ.一方,n=10, K=21という設定では,#=6で cycle={10,16,13,4,19,1,10,}が表示される.ただし,ψは空欄になっている.つまり,nにある値を設定し,KとBに同じ値を代入すると,上の状況を再現できる.いや,違う.べき剰余画面では B→n, n→K のように設定しなくてはならない.
この2つの逆向きの計算を一画面に同時に表示することはできるだろうか?nが除数Kに向かうところが難解なところだ.パラメータの名前が誤解を招き易い.Bはbaseで自明だが,nは対象数,Kは固定の除数のイメージがあり,Kをnとみなすこと自体に抵抗がある.KをΘで置き換えてみよう.小文字のθは角度として普遍的に使われているが,大文字のΘはあまり使われていない.この文字を選んだ理由は割り算記号÷に少し似ていないこともないという理由だ.Ξが111を90度回転させたものと似ているというのと似たような理由だ.
そうなるとnの方にもギリシャ文字を割り当てた方がよさそうな感じになってくる.どうせなら,Bをβとし,nをαとしてみてはどうだろう?αとβは同格なので互いに入れ替え可能というイメージになる.べき剰余と逆数の循環小数を連通させるというのがこの検定の最大の目的であり,それにそうとすればこの辺りを明確にする必要がある.α/βではなく,A/Bというのでもそれほど悪くはないような気はする.そうなると,指数のeもギリシャ文字でεではないだろうか?QとRは英字で残ってしまうが,仕方ないだろう.今後はこの記法に従って記述することにする.
εには固定のイメージがあるので使いづらい.α,βの次の文字γを割り当てることにしよう.γはstripeに関係する.縦数列はまだあまり深く調べられていないので,これから発展する領域と考えられるので,α, βと同格の文字を割り当てておくのは適当だと思う.
2つ問題がある.(1)α=21, β=10とするとU=47619, αU=999999で6桁なので@=6, また,αとβを入れ替えてα=10とし,Θ=21とすると,#=6, cycle={10,16,13,4,19,1}となって,上の記述と合っているが,ψの値が不定になっている.(2)U=47619*x and r=x, then the equation holds for any x という問題.
ここでGet ψを実行すると,Θは11に代わり,ψ=2が表示される.これはどちらかが間違っているかないし,異なる定義によっていることになる.ψ関数(u-length function)の定義に戻ってみよう.
Given mutually prime numbers n and b, there exist nonnegative integer x<n and positive integers y and z such that z=x*b^y \n…x, that reads n divides x*b^y, the quotient z, and the remainder x, in other words, n*z+x=x*b^y. A set of {x,y,z} exists infinitely. u-length function y(b,n) is defined as the minimum such number y, as well recursion unit U(b,n) as the minimum such number z.
今の事例では,n=21, b=10, z=47619, y=6 のはずだが,合っていることを確認しよう. 21・47619+x=10^6・x → (10^6-1)x=999999\x=21・47619=999999 ∴ x=1 確かに数値的には合っているようだ.ψ(b,n)の値はそのような関係式を満足する最小のyとされているのだから,ここではψ値は確定している.現行ツールでψ値をどのように決定しているかを見てみよう.⇒PsiFunctionでは,φ(α)の約数からψを割り出している.今φ(α)=4なので,約数列は{1,2,4}
10^1%21=10, 10^2%21=10, 16, 10^4%21=4でR=1が出てこない.なるほど,理由はわかった.ψがφの約数であるというのは正しいが,ψ=φの場合があることを見落としている.これを入れれば多分解けるはずだ.いや,間違いだ.φ=4は計算には入っている.ψがφの約数であるという推論が間違っているのではないだろうか?いや,これは定理ということになっている.
P1(T):For any natural number n>2 on b-base decimal system, the value of u-length function y(b,n)>0 always divides the value of Euler’s totient function f(n), i.e., gcd(f(n),y(b,n)) = y(b,n). If n is a prime, then y(b,n) divides n-1.
どうもこれが間違いの元ではないだろうか?Wolfram MathWorldのMultiplicable Orderの項目によると,10^6≡1 mod 7なので,ord_7(10)=6となっている.φ(10)=4なので,ψ=6はφ=4を割り切ることはできない.確かに現行プログラムではこのような場合には「互いに素でPSI検出不能」というメッセージを出している.
https://mathworld.wolfram.com/MultiplicativeOrder.html
応急的にαのすべてのべきをテストするように修正して動作するようになった.この論理はもし,cycle数列が手元にあれば,もっと高速化することができる.マトリックスの一行だけを出力する手立てはあるだろうか?⇒周期数列はDispResidueCycleで表示している.この関数はResidueFuncProから呼び出されているが,この数列を得るためにはPowerResidueFuncを実施することが必須だ.PsiFunctionは剰余演算とは独立に実行できなくてはならないから,独自にcycleを取得できるようにするべきだろう.これはBuildMatrixでやっていることの一部を切り出すことに当たる.⇒GetResiduCycleという関数を作った.これでψ値の計算にはFactoringが不用になり,無茶苦茶高速化された.
やはり,ψがφを割り切るというのは完全な誤りであるように思われる.α=29でΘ=59のとき,φ=28でψは29になる.剰余数列は下記のようなものになっている.
{29,15,22,48,35,12,53,3,28,45,7,26,46,36,41,9,
25,17,21,19,20,49,5,27,16,51,4,57,1,29,}
αは29で素数だから,φは当然28になる.このとき,ψ値は29でφよりも大きい数になっているから,当然φを割り切ることはできない.Θがαよりも小さいときにはもしかするとψがφを割り切るということが成立しているのかもしれないが…いずれにせよ,何らかの条件がなければ成立しないものと思われる.⇒非常に重要なことを発見した.これは以前にどこかに書いたことがあるような気がするが,αとUはある基数Bの進数システム上で「逆元」であると言える.下図を見ると,このことが疑問の余地なく確認できる.
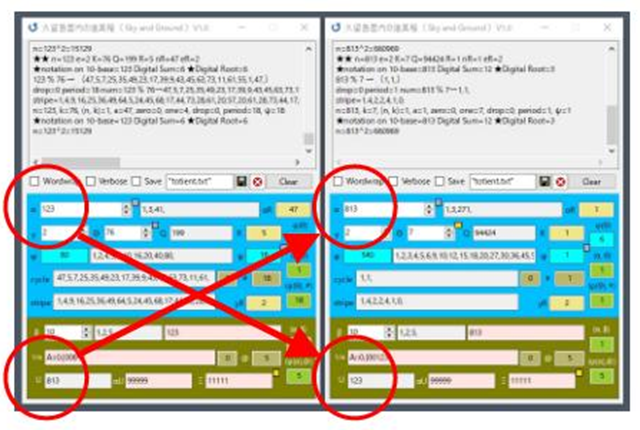
いや,逆元と言うからには,a ✕ a^-1=1となることを証明しなくてはならない.確かにそんな簡単なものではない.123 x 813 = 99999だ.これを見て言えることは,99999を単元とみなすことができれば,確かにこの2つの下図は互いの逆数であると言えるだろう.仮に999…999のような形のすべての数を単位元とみなすとしても,999…999の約数とならない数はいくらでもあるはずだ.Wolfframのページには下のような表が掲載されている.この程度のものは出力できるようにしておきたい.
Multiplicative Order
▲Get ψはほとんど不用になった.
▲道具箱から複数の画面を開けるようにする.ないし,出力画面を道具箱に移す.⇒完全に2つの(等サイズの)ウィンドウに分割した.
これしかない.タブにしてもよいのだが,そうすると出力画面とパネルを同時に見ることができない.出力画面は不用なときには閉じてアイコン化しておくことができる.道具箱を閉じるとアプリ終了する.
▲原始根マークが間違っているようだ.α=123488でΘ=5のとき,αにマークが付いているが,cycleは0#0で3.と表示されているだけだ.そもそもcycleの表示がおかしくなっている.どこか壊してしまったのだろうか?cycleを表示しているのはDispResidueCycleだ.この関数に渡されるdropとperiodが間違っているのだろう.おかしい.こんどは正しく表示されている.開始時点のα=123456,Θ=7に戻ってやり直ししてみよう.途中で巨大なレピュニット数が出現しているのが関係しているのかもしれない.6498桁もある数をダンプするというのが無茶だ.MakeRecursionUnitでも巨大数をダンプしている.
現在MakeRecursionUnitではMAXTEXTLENGTH=32767を上限としているが,さすがに大き過ぎるのではないか?MaxOutput=10000に落とした.だいぶ楽になった.
▲Θ=8でαを変えていたら,α202の辺りでハングしてしまった.kinaiは3つ走っている.VS19も2つ走っている.⇒制御が戻ってきた.イベントが滞留してこなすのに時間が掛かっていたためだ.
▲cycleは重複しない文字列でよい.(末尾の1文字は余分)桁数#分だけ出せばよい.
▲cycleのdropと1/αのfixedに記号を与える.⇒使える余白がないので,現状のままとする.無名の値を参照するときには [3#12],[0@23]などのように表記して区間に関係する値であることを暗示すればよい.