現行ではすでに垂直セグメント検定(TestVerticalSegment)という処理は廃止(2018/02/26)されているので,垂直スプリットが発生したときそれを補正する手段は存在しないが,AFTERMARGSAMEGENEフェーズでShiftDirectAbsoluteの実行を抑制すれば垂直スプリットの発生を回避することはできる.これは重婚同類検定ですべてのノードの垂直位置(世代)を事前に決定しているためと考えられる.しかし,循環性多重が存在するときには重婚同類検定の結果をまったく使えないというのも過剰であるように思われる.重婚同類検定をもう少し深堀りして,「寸止め」のところまでは実行できるようにしたい.
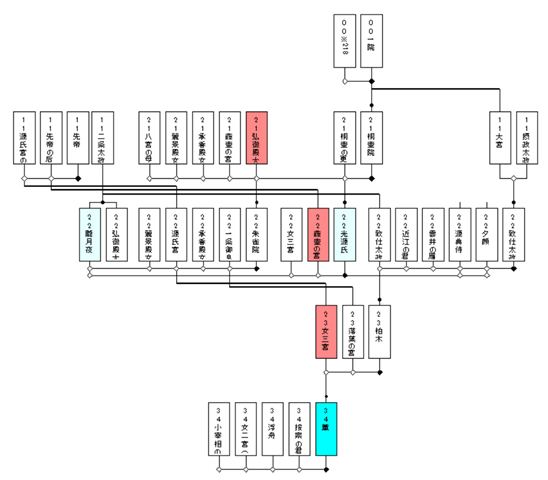
目的は「多重カード出現の極小化」にある.実際,昨日の反例サンプルを見ると,少なくとも2枚の多重カードは削減できるように思われる.多重カードの削減はメインループの中でも動的にTOPOLOGY:ReduceMultiCardを使って実施しているはずなのだが… なぜそれが利かないのか調べてみたところ,多重カード数が不可避の多重カード数と同じになるとブレークしていることがわかった.この「不可避の多重カード数」を強制的に-2してループするようにして,下図を得た.
多重カード数は5から3に減少している.重婚同類循環の件数は3なので明らかにこの図面がこれ以上多重カードを削減できない極限に達していることは明らかだ.つまり,この図面は少なくともこのサンプルに限って言えば,「完成図」であると言える.TribeRelocationのステージ【7.8】多重カードゼロを検査して変化なしなら検定打ち切りの打ち切り条件を多重不可避(Inevitables)から重婚同類循環(sameGeneCycles)に変えることでこの動作を一般化できる.しかし,これだけでは多重を極小化することはできない.
たとえば,光源氏の全体図では重婚同類=3であるにも関わらず,多重カードは16も残ってしまう.このとき,多重不可避は8となっている.まず,これらの用語の意味をもう一度確認しておこう.重婚同類循環(sameGeneCycles)はTestInevitableMultiZeroが返す値で,重婚同類循環の発生件数と考えられるが,かなりルーズな扱いを受けているのでもう少し整理する必要がある.sameGeneCyclesは以下のポイントでインクリメントないしセット/リセットされている.
- TOPOLOGY::ResetExperiment 初期化
- TRIBERELOCATIONフェーズ入口 リセット
- SIMPLENODE::MakeOyakoEda(多重グラフ2)
自己ループでカウントアップ - BuildSameGeneMarriageGraph(多重グラフ2)の結果を加算
- SameGeneMarriageCirculationの結果を加算
- TOPOLOGY::TestInevitableMultiZero
除去したループ枝の個数をカウントアップ - TestInevitableMultiZeroの結果をセット
どうもあまりわかり易くない.重婚同類検定では枝グラフを3つ使っているのだが,それぞれの構成/用途を確認しておこう.
- 多重グラフ1(tajugraph1) 節点:人名カード,枝:婚姻関係(単身婚の場合は自己ループ),複数親を持ち子どもを持たない終端ノードの自己ループ枝,連結成分:婚姻関係によって連結するカード集合
- 多重グラフ2(tajugraph2) 節点:重婚同類(グラフ1の連結成分),枝:親子関係(親の含まれる連結成分と子の含まれる連結成分を結ぶ)自己ループを削除しsameGeneCyclesに加算する,冗長枝を除去する 連結成分:親子関係によって連結する重婚同類の集合(重婚同類族)
- 多重グラフ3(tajugraph3) 節点:グラフ2の連結成分,枝:親子関係(グラフ2の枝)
これもまた,あまりわかり易いものではない.特に多重グラフ3と2の違いがよく分からない.グラフ3の枝がグラフ2の親子関係であるとすれば,すべての枝が自己ループになってしまうような気がするのだが… ここではグラフ3 をハッセ図と呼んでいるようだが,その意味も不明だ. SIMPLEGRAPH:TightenHasseDiagram では出口でグラフ2の除去された枝をすべて元に戻している.BuildTightHasseDiagramでは静定するまでこの関数を呼び出しているのだが…
しかし,この部分を読み解かないことには始まらない.グラフ1を婚姻グラフ,グラフ2を重婚グラフ,グラフ3をハッセ図と呼んでおくことにしよう.1の婚姻グラフに2種の自己ループ枝が追加されている理由が分からない.重婚同類を見るためには婚姻関係と親子関係の両方を見る必要はあるが,なぜ単身婚を加える必要があるのか?世代を確定するためには必要になってくるという可能性も考えられるが…
2の重婚グラフの目的は重婚同類循環(sameGeneCycle)の個数を確定することにあると考えてよいだろう.しかし,カウントを持ち寄って合算するような判り難いものになっている.3のハッセ図の目的は多重を除去した状態で絶対世代番号を確定しようとしているものと解釈されるが,毎回枝を除去してまた戻すという操作の意味がよく分からない.
ハッセ図はとりあえず置いて,重婚同類循環(sameGeneCycle)を確定することを考えよう.重婚グラフのノードである重婚同類が親子関係としての自己ループを持つとすれば,重婚同類循環に当たることは明らかだが,親子関係によって連結した連結成分要素である重婚同類族それ自体はただちには重婚同類循環には当たらない.それをどこで見ているのかをチェックしておこう.
最初にsameGeneCyclesをカウントアップしているのは,BuildSameGeneMarriageGraphだが,ここの処理で分かりづらいのは,この関数の内部ですでにsameGeneCyclesを一部カウントアップしているという点だ.これは改めるべきだろう.この関数はカウンタloopedgeの値を返しているが,AddOyakoEdaの中ですでにsameGeneCyclesをインクリメントしている.SIMPLENODE:AddOyakoEda→MakeOyakoEdaでは自己ループになったときにはその枝のselfloopフラグをオンにしている.
BuildSameGeneMarriageGraphではこの後,自己ループ枝を削除するときにloopedgeをインクリメントしているので,重複カウントされている可能性がある.⇒この修正で重婚同類個数は2になったが,多重カード3が残る.メインループはトポロジーが変化しなくなると多重が残っていてもループを抜けるようになっている.見たところいずれも「不可避の多重」のように見える.重婚同類循環が2つであるとすれば,その構成要素を特定できなくてはならない.重婚同類循環の検査はSameGeneMarriageCirculationで実施している.しかし,この検査では循環は検出されていない.SameGeneMarriageCirculationではTestStronglyConnectedでグラフを「強連結成分に分解」している.
サンプルとして用いている薫のZ木家系図では重婚同類循環数は2となっている.一つは自己ループ(桐壷院→光源氏)だが,もうひとつはなんだろう?TestStronglyConnectedは3箇所で使われている.一つはSameGeneMarriageCirculationの中であとの2箇所はTOPOLOGY:TestInevitableMultiZeroだが,いずれも無反応だ.ただし,TestInevitableMultiZeroではtajugraph2->selfloopの値をsameGeneCyclesに追加している.これはおそらく前にカウントした値が残留したものと推定されるので,おそらくカウントの重複と思われる.selfloopcountで数え直ししてみることにしよう.
自己ループが1残っている.ただし,これはすでに削除された枝だ.削除と言っても現物はそのまま,「削除された」というマークが付いているというだけだが,selfloopcountはマークを無視してカウントしている.このルーチンを修正して,自己ループカウントはゼロになったが,今度はTestInevitableMultiZeroのステージ【14】強連結成分の抽出で削除した枝を戻すの段でカウント不一致が発生するようになってしまった.この関数は元の仕様に戻した方がよさそうだ.その代わり,sameGeneCycleにloopedgeを加算ではなく,代入とするのが正しい.
結局,重婚同類循環=1で多重カード3という結果になった.しかし,これでもまだあいまいさが残る.重婚グラフの枝集合に含まれる自己ループは重婚同類循環に関わるものだが,必ずしも一対一という訳ではない.自己ループ以外の循環はSIMPLEGRAPH::TestStronglyConnectedで検査しているが,この検査では「行き止まりノードの枝をグラフから削除する」ということを実施しているだけで,もし枝が残ればそれは重婚同類循環に含まれる枝ということになるが,この場合はサイクルを構成する枝集合と重婚同類循環が対応するということになり,やはり一対一の対応にはなっていない.整理すると以下のようなことになる.
- 重婚グラフの枝集合の中の自己ループ枝は重婚同類循環に関係する
- TestStronglyConnectedで除去されなかった枝は同類循環に関係する
ということになり,重婚グラフの枝集合を見ても確定的な情報は得られない.連結成分はノードの集合であり,それらがどの枝に関わっているかということは直ちには分明ではない.TestInevitableMultiZeroの出口で重婚グラフをダンプすると,節点数=6 枝数=7 有効枝=6 removed=1 nouse=0 usable=0 selfloopcount=1という結果になった.接点数6というのは重婚同類が6個あることを意味する.枝数7でうち有効枝数6というのはremovdeが1あるためだろう.selfloopcount=1というのは枝リストをスキャンして得た値だろう.7つの枝のうち,removedとselfloopのものが1つある.
SIMPLEEDGEには,selfloop,removedの他に,usableというメンバー変数がある.これには閉路上の枝というコメントが付いているので,これを利用することにしよう.いや,この変数は「有効枝」という意味で使われているようだ.今の場合はこれと真逆な使い方になる.「冗長枝」という意味で使われることもあるようだ.この他にnouseという変数もある.これには「切断された枝」というコメントが付いている.removedとどういう違いがあるのだろう?nouseというのは連結成分への分解で使われているようだ.
SIMPLEEDGEにcircular // 循環する枝(閉路上の枝)という変数を追加した.また,SIMPLEGRAPHにcirculars // 循環する枝数(閉路上の枝,自己ループを含む)を追加した.