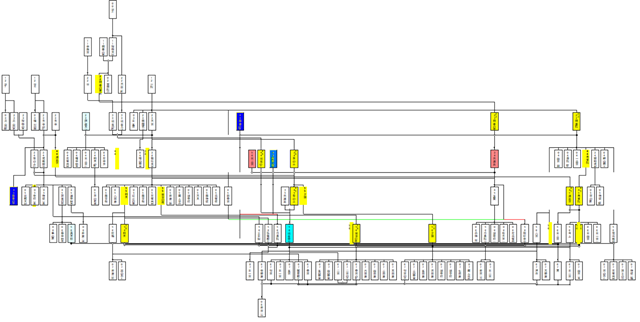
系図作図上の要点は多重カードの出現を極小化することにある.カード多重の原因が重婚クラスタ循環の存在にあることは2017年初頭にはすでに突き止められていたが,それから四年経過した今もなおパーフェクトな解法は得られていない.つまり,重婚クラスタ循環が存在しないときに多重カードゼロの図面を描画することはできているが,クラスタ循環が存在するときの多重カードの最小化には成功していない.と言うか,この部分は手つかずで放置されていた.今回はこの「系図作成上の最大の課題」に最終的な決着を付けたいと思う.
配偶関係(婚姻関係)によって相互に連結したカードの集合を重婚クラスタと呼ぶ.配偶関係は排他的な同値類を構成するので,ある重婚クラスタに属するカードが他のクラスタに属するということはあり得ない.サイズが2より大きいクラスタがあるとすれば,そこには必ず一人以上の重婚者がいると考えられる.重婚クラスタを節点とし,親子関係を枝とするグラフを重婚グラフBとする(クラスタCに属するカードPの子どもQがクラスタC’に入っている場合,C→C’の枝が生成される).親子関係には方向性があるので,グラフBは有向グラフであるとする.
グラフBが循環(閉路)を含んでいないときには,多重カードの存在しない図面が描画できることは明らかである.グラフBの連結成分を重婚クラスタ属とする.重婚クラスタ属とは親子関係によって垂直に連結された一群の重婚クラスタの集合である.有向グラフは任意の2節点間に有向経路が存在するとき,強連結であると言う.強連結グラフ上の任意の有向枝は必ずいずれかの有向閉路上にある.
※重婚クラスタ属とはZTシステムの用語で言えば「系統」に相当する.つまり,始系列と直接/間接に接合した複数の系列の集合と等価である.
有向グラフBの重婚クラスタ属Gが強連結であるか,強連結成分を含んでいる場合,つまり,クラスタ属Gが循環(閉路)を含んでいる場合には系図図面上には多重カードが発生することは避けられない.これを不可避の多重カードと言い,多重カード発生の要因となるようなクラスタ属に含まれる強連結成分(孤立ノードを除く,ただし自己ループを持つノードを含む)を重婚クラスタ循環と呼ぶ.
重婚クラスタ循環(循環を持つ重婚クラスタ属に含まれる強連結成分)から循環の要因となる親子枝を除去することにより重婚クラスタ属が循環しないようにすることは可能だが,一般に,このような枝(循環枝と称する)を除去しても事態は何ら好転しない.というのは,重婚クラスタ循環の要因となる「循環枝」はほとんどの場合,「自己ループ」であるからだ.と言うか,手持ちサンプルでは例外なく自己ループであるとしてもよいのではないかと思われる.
親子枝が自己ループになるというのは,ある重婚クラスタの中に親とその子どものカードが同時に含まれている場合に発生する.婚姻関係ないし配偶関係にある2つのカードがつねに同世代に配置されなくてはならないことと同様に,親子関係にある2つのカードでは少なくとも親カードは子どもカードよりも上の世代に配置されなくてはならないことは明らかだ.従って,親子枝が自己ループになるとすれば,この婚姻の水平的関係と親子の垂直的関係が直交する(両立しない)矛盾と言える.
重婚クラスタ内のノードは同一世代に配置することが求められているが,それが不可能であるとすれば,クラスタを一度世代別クラスタに分割する以外の方法はない.その方法を考えてみる.
- 重婚クラスタ循環から循環がなくなるまで親子枝(P, Q)を除去する
- 重婚クラスタ循環から除去された枝の集合を循環枝集合Sとする
- 重婚クラスタ循環に含まれるカードを節点とし,配偶関係を枝とする無向グラフを循環グラフJとする 仮定により,グラフJは連結であるが,内部に閉路を持っている場合もあり,持たない場合もある
- 枝集合Sから循環枝を1個取り出し,親子枝(P, Q)とする.
- ノードPないしQのいずれかがグラフJに含まれない場合はステップ8へ
- 枝(P, Q)の親ノードPと子ノードQを分離するようなグラフJのカットセット(切断枝集合)を求めて,グラフJから除去する
- 親ノードPを含むパートに含まれるノードをグラフJから除去する
- ステップ4に戻って枝集合Sが尽きるまで繰り返す
- ステップ5のカットセットに含まれるすべての枝を元の検定グラフ1から除去して,重婚クラスタ検定を再実行する
この解析の目標はステップ6のカットセットを最小化することだが,おそらく,除去されたカットセットの枝数と表示される多重カード数が(ほぼ)対応するのではないかと推定される.カットセットが最小であることを求めないのであれば,カットセットの枝集合を決めるのは簡単だ.親ノードPの周辺の枝をすべてカットすれば,Pは孤立ノードとなり,Qはそれ以外のすべてのノードと連結したままになる.その逆に,最小カットセットを求める問題はNP完全ではないかと思われる.たとえば,2つのパートの節点数が等しくなるようなk-カットセットが存在するか否かを問う問題はNP完全であることが知られている.※
※グラフの節点を2つのパートに任意に分割したときのカットセットを求めるのは難しくない.かき混ぜた納豆をスプーンにすくって取り分けるときに長く伸びた糸をくるくるっと回して切れば,それが「カットセット」であり,どのような分割でもカットセットは一意に決定できる.
次善の策として,ノードPから距離1だけ離れた枝を削除するということが考えられる.ノードPに隣接する枝はすべてPの配偶者だが,その次の枝はPの配偶者の配偶者への枝になる.事例から見ると重婚クラスタ循環の親子枝の親となるようなノードは通常重婚者であり,それも多重婚者である場合が多い.たとえば,桐壷院は配偶者を6持っているし,光源氏は13も持っている.従って,Pの隣接枝をカットするやり方では最小どころか,最大カットセットになりかねない.Pの配偶者が重婚者である可能性はゼロではないが,確率的にはそれほど高くない.
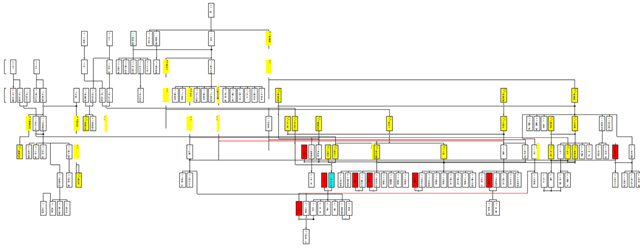
もし,この方式でよいとすれば,グラフJを新たに起こさなくても,元の検定グラフ1上で操作できるかもしれない.実装はそれほど難しくないので,試してみることにしよう.⇒うまくいったようだ.多重は3件まで減少した.まだいくつかエラーが出ているが,描画はほぼ完璧だ.
画面の下の方にあった多重は完全に解消した.下図は修正前のバージョンで描画したものだが,これまでは本来クラスタ循環と関わりのない部分で多量の多重が発生していた.これは重婚クラスタ循環で生じる世代的な矛盾が放置されていた(重婚クラスタ循環を世代分割していなかった)ためだ.今回はごく一部の不可避多重を除外してすべてのカードの世代が確定しているので,このような多重の発生する余地がない.