コラッツからゼルコバの木にインポートするという操作がある程度滑らかに実施できるようになってきた.ここまでできると,次はインポートしたファイルをPDFに落として,かつ左90°回転させ,文字が正立した図面として保存したい.PDFの回転はChromeでもできるが,保存ができない.ダウンロードはできるが,保存されたファイルを開くと回転が戻ってしまっている.保存という機能もあり,たまたま保存できたケースもあるが,その手順が確立できない.CubePDFに印刷出力するという手もあるが,やはり回転が戻ってしまう.AdobeのAcrobat Reader DCの有料版なら回転までサポートされているが,買取りではなくサブスクリプションで月2千円も掛かるのでは手が出ない.ゼルコバの木でそこまでできるようにする必要はあるのだが,今日明日というわけにもゆかない.⇒いや,できた!多分この手順で間違いないと思う.
- コラッツからCSVファイルをエクスポート
- ゼルコバの木でファイル→隣接リストをインポート
- プリンタにCubePDFを選択,用紙サイズをA0に設定
- 拡大縮小倍率を調整して1ページに収まるようにする
- CubePDFに印刷出力してPDFファイルに保存
- ChromeでPDFファイルを開き,画像を回転させる
- 印刷画面を開き,送信先をCubePDFに設定
- 詳細設定で用紙サイズをA0,倍率は既定
- CubePDFで印刷→PDFに保存
ダメだ.確かに回転は保存されているが,図面の上半分しか入っていない.LibreOfficeでPDFを読み込んで回転まではできる(かなり時間が掛かる).しかし,図形を拡大縮小操作しているうちにフォントが荒っぽくなってしまうという欠陥がある.⇒最初に図形を全選択してからフォントをメイリオに切り替えておくと多少よい結果になる.図面を回転させたあとはページ設定でページサイズを整えたあと(オリエンテーションを横から縦に変えてもよい),ドラッグ移動してページの中に収まるようにすればよい.まぁ,これなら↓なんとか使えるだろう.
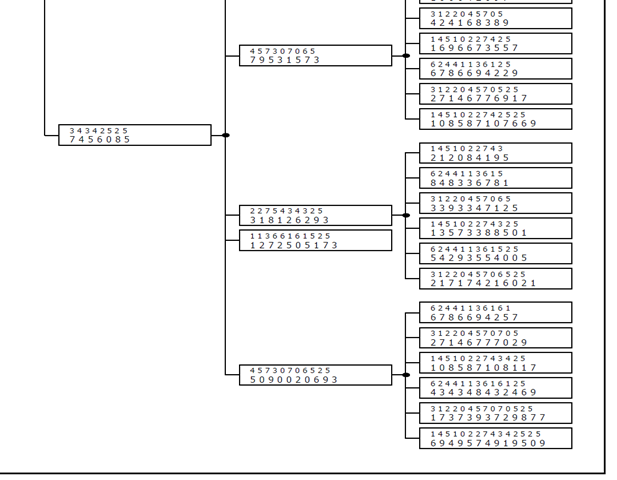
上図は1-3-4 511コラッツ木で所属の欄に8進数表示のノード番号を表示している.これを見ると,8進で末尾が5なら非コラッツ数であるということが一目瞭然にわかるが,01の並びを見れば第何子であるかわかるはずなので,それも見られるようにしてみたい.このためには8進ではなくむしろ4進表示が適しているのではないだろうか?ちょっとやってみることにしよう.できた!
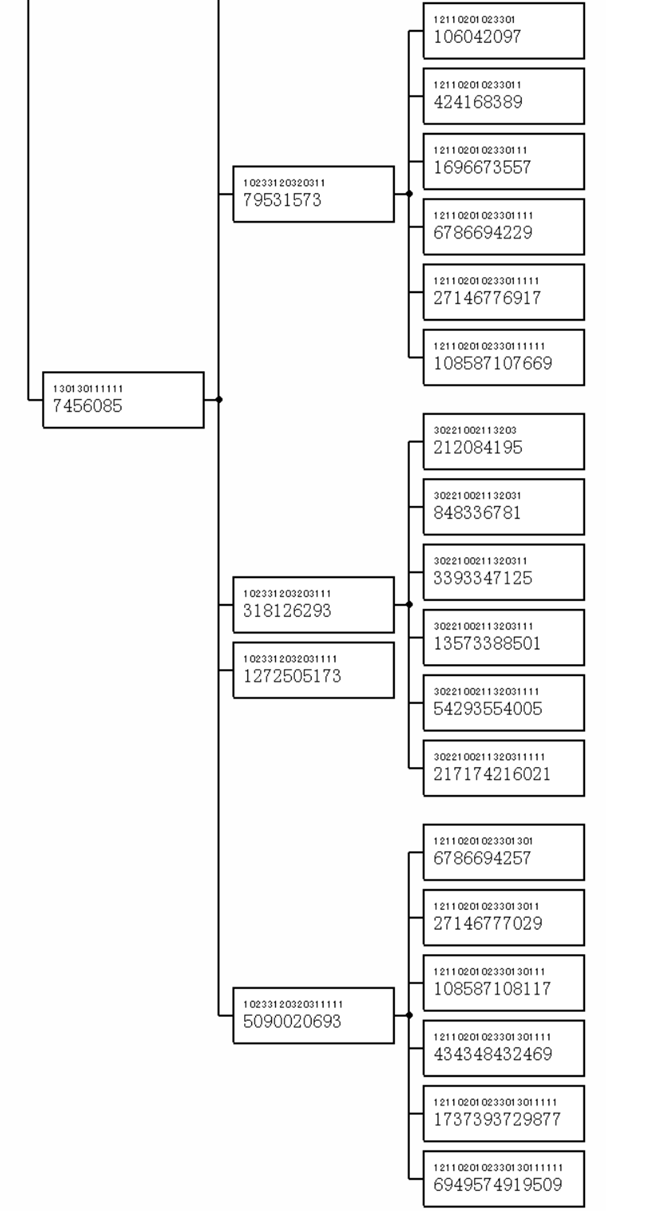
これはかなりわかり易い図だ.兄弟順位がそのものずばり,4進表記したノード番号に現れている.しかも,4進表示すると,これらの兄弟ノードの名前の語幹部はそのものずばり親ノードを示しているように読める.つまり,すべての兄弟が同じ「姓」を持っている.例として5090020693の子ども枠の中を見ると,第1子が12110201023301301で,第2子は12110201023301301-1,第6子は12110201023301301-11111.親の5090020693自体は,5090020693の6番目の子どもで,102331203203-11111という4進名を持っている.長子12110201023301301の名前には2のべき乗数が入っていたはずだが…一昨日の記事から再掲すると,
P=F(S)=(3S+1)/2 c=1の場合:S=…011, …111の場合
=(3S+1)/4 c=2の場合:S=…001の場合
=(3S+1)/16 S=5=101の場合
ということになっているので,4進表記すると,c=1というのは,末尾が3,c=2は1,c=4はS=5しかないので,S=11という場合に限られる.末尾が0ないし2なら偶数だから,末尾が1ならば,c=2,3ならc=1.ノード番号全体が11ならc=4ということになる.cの値が決定できれば,あとは3S+1を計算し,それを2^cで割ってやれば親数を得ることができる.もし,3進数で表示されていれば,3N+1がどんな数になるかはすぐ分かるが,それを2のべき乗で割り込んだ結果は子ノードの名前とはかけ離れたものになるのは避けられないだろう.
それにしても,兄弟の氏名がこんなにシンプルな構成だということを想像したことがあったろうか?これはもはやコラッツ問題が完全に解かれたということの証左以外のなにものでもない.子ノードの3S+1という数を計算してそれをバイナリ表示してやれば,この辺りの関係もある程度見えてくるのではないだろうか?それをやってみよう.
この値を生没日付欄に表示してやろうとしたのだが,出てこない.本来日付は内部的には文字列としてしか扱っていないはずなのだが…日付データとしての有効性をどこかでチェックしているのだろう.仕方ないので肩書欄に記入してみた.長くなってしまうが,仕方ない.
もはや,これ以上のことを言う必要はないだろう.子どもノードSのノード番号に3S+1という変換を掛けて得た数値はそのものずばり,親ノード番号+右シフトの回数になっている.この兄弟ノードの親ノードである5090020693を4進表記した数字はすべての子どもノードの4進表記の中に埋め込まれている.また,子どもノードSの3S+1のバイナリ表現の中にも完全に親ノード番号が埋め込まれ,それを2^c倍したものになっている.明らかにこれは一種の戸籍システムであり,あるノードのノード番号がわかればそれを順繰りに手繰って,先祖ノードまで遡ることができることは明らかだ.これは家系図を作成するときに本籍地から本人の戸籍→父の戸籍→祖父の戸籍を手繰るのとまったく同じ手順である.4進表記と3N+1の2進表記の間に,3進表記というのを挿入すれば,計算するまでもなく,子ノードのDNAが親ノードのDNAを正確にコピーしたものであることが分かるだろう.この図面はほぼ,コラッツ予想問題の「完全な証明」に相当するものになっていると思う.
親ノード5090020693を2進表記すると,100101111011000111000110101010101のようになる.その子どもの6949574919509の3N+1を2進表記したものは
100101111011000111000110101010101000000000000
のようになる.この末尾の0を取り除くと,100101111011000111000110101010101となって完全に一致する.これは計算の結果そうなったのではなく,もともと埋め込まれていたものであることを示すにはやはり3進数表記を見るのが一番早いと思う.やってみよう.⇒いや,ダメだ.思ったような結果にはならない.当然かもしれないが,3進表記した場合には兄弟ノードのすべてで異なる名前が生成され,共通部を見出すことはできない.これをやるとしたら,長子木を使った方がよいかもしれない.長子ノードの3進表示を左に1シフトして1を加えたものを2ないし4で割ったものが親ノード数になる.従って,親ノードを2ないし4倍したものから1を減じたものを3進表示すれば共通部が見えてくるのではないかと思う.これは長子木が復活したあとで試してみることにしよう.「親ノードを2ないし4倍したものから1を減ずる」のような操作は一種の「計算」ではあるが,2進ないし4進数としてみると,これはDNAの文字並びを壊さない操作になっているので,それと子ノードの3進数が共通部を持つことを示すことができれば,「DNA保存」という文脈の中で説明可能になる.
我々の意図するところは,子ノードが親ノードのDNAを引き継いでいること,そのDNAシーケンスから先祖ノードまでの遺伝子継承関係を手繰ることが可能であることを示すことにある.その目標はすでにほぼ達成されているのではないかと思う.4進表記したときの下位ビットはそのノードの兄弟順位を示すものであり,たとえば,太郎・次郎・三郎などのような一般的な呼称になっている.上位ビットは親の名前だが,暗号化されているため親の実名とは一致しない.しかし,すべての兄弟が同じ親の名前を共有していることは確かだ.親ノード番号を親の実名とすると,子ノードの中に埋め込まれている親の名前は親の戸籍名(暗号化された実名)であると言える.しかし,暗号化された親の実名をデコードするのは難しくない.そして,親の実名もまた,親の親の戸籍名+太郎・次郎などの兄弟順位名から構成されている…結構単純な仕掛けだが,我々が「アドレスコード」と呼ぶものと「ノード番号」が完全に等価であることの実証であると言ってよい.
一言でまとめれば,「自然数の原戸籍簿は4進数によって標記されている」ということになるだろう.4進数のアルファベットは0, 1, 2, 3の4文字である.ここでピンと来たあなたは確かにいい感をしている.人間に限らず,すべての生物のDNAがACGTの4文字から構成されていることはよく知られた事実であり,自然数の4進数表記がDNA配列になっていることはいまさら驚くべきことではないのかもしれない.