未公開だが,コラッツ木ジェネレータ最終版のタイトルは,Collatz Complete Tree Experiment(コラッツ完全木検定)となっている.「完全木」とは「完全正則木」を略したもので,英訳すれば Full regular tree になる.正則グラフとはグラフのすべてのノードの次数(隣接する頂点数)が等しいものを言う.有限木の場合には必ず次数1の終端ノードを持つから正則木というときには,「終端ノードを除き」という追加規定が入る.ただし,完全正則木と言うときには終端ノードは木の最下層(最上階)にしか現れないものと仮定する.一般コラッツ木では3倍数が木の各所に現れるので,完全正則にはならない.
どうも,開発者であるわたし自身の中で「完全木」と「仮想木」の違いがあいまいなものになってきている.コラッツ仮想木とは,別名「コラッツ長子木」と呼ばれるもので,一般コラッツ木上の親ノードを共有する「兄弟ノード」を最上位の「長子ノード」1点に集約した簡約グラフを意味する.3倍数も長子ノードとなることはあるが,その下には兄弟ノードの子ノードが配置されるので,終端ノードにはならない.この意味では仮想木は完全正則であると言える.
▲コラッツ完全木検定のA面で1-3-4の設定で生成されたコラッツ木のCSVをインポートしようとして,「入力文字列の形式が正しくありません」というエラーになった.
開くファイルを間違えていたかもしれない.生成されたCSVはCollatzTree.C.csvだが,別のファイルを開いていた可能性がある.実際,”CollatzTree.C.csv”は正しく開けた.多分ZEL形式のCSVを開いていたのだろう.デスクトップ上にある,CollatzCore.CSVを開くとこのエラーが出る.CollatzTree.CSVでも同じ.CollatzTree.CSVはこれまで何度もインポートしていたような気がするのだが…テキストエディタで開いてみると確かに,これらはZELの一覧表形式CSVだ.⇒間違え易いのでZEL形式CSVは別のフォルダに移動した.
▲隣接リストCSVをインポートするとき,中間的にZEL形式CSVが生成されている.これは作業用の一時ファイルなので使い終わったら削除しておく必要がある.⇒このファイルは動作確認の意味を含めて温存していたが,「一般的な(順序不定の)隣接リストで正しく動作する」ことが確認されれば削除されるべきだ.
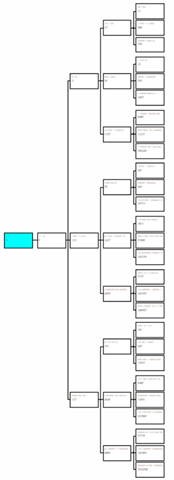
コラッツ完全木と仮想木の相違点がわかった.下図で左が仮想木,右が完全木と称するものだ.どちらも1-3-4という設定で出力したものだが,前者が41点に対し,後者は121点ある.
後者は厳密に完全3元木になっているが,前者では1階層目に1個しかノードが存在しない.確かに,これが「仮想木」という構成の特異な点だったのを想い出した.この5というノードの特殊性はコラッツ木を理解する上では重要なポイントであり,おそらくこの点を強調することが,三本桜を復活させる動機の一つになっていたのではないかと思う.ログをもう少し読んでみればその辺の事情もわかってくるだろう.
もう一つの用語として「コラッツ核木」ないし「コラッツ中核木」というのが出てくるが,これはコラッツ長子木の別名と考えられる.つまり,コラッツ仮想木=コラッツ長子木=コラッツ中核木と考えられる.いずれかに統一するとすれば,コラッツ長子木というのがもっとも直感的なのではないだろうか?「長子木」は「長子ノード」のみで構成される系図木であるという説明は,「なぜ仮想木と呼ばれるのか?」あるいは,「なぜ中核木なのか?」を説明するよりわかり易いような気がする.「仮想木」と呼んでいるのは,仮想木上のノードを接続する枝が,「コラッツ写像」を直接反映した「実像」になっていないためだ.
「長子ノード」はときに「コラッツ数」と呼ばれることもある.コラッツ数として区分される整数の集合が,コラッツ木の骨格であり,それ以外は葉肉であるというのが「コラッツ中核木」の由来と考えられる.ルートが5であるようなコラッツ中核木(の部分木)を考えると,これは完全正則木を構成可能である.つまり,コラッツ中核木からノード1を除外した部分木は完全正則木の条件を満たしている.
しかし,我々の「コラッツ完全木」はノード1を含んでいる.その構成原理を明示しなくてはならない.⇒その前に「コラッツ放射高速道路系」という概念が登場する.「木」は通常「ルートノード」を根とする樹状の図形として描画されるが,ルートを中心とする放射線路系として描画されてもよい.この意味ではコラッツ木とは1/5を始点として放射線状に投射される交差しない数直線の集合とみなすことができる.
ルート5から投射される放射線は無数にあり,1本の放射線上には無数の点がある.これらの無数の点はそれ自体が放射の中心点となって全方向に無数の放射線を投射している.5をルートとする完全正則木の終端ノードはすべてルート5から等距離にあると考えられるから,これらの集合は1個の3次元的な球面上にあると言える.この放射線を光線とみなせばコラッツ完全正則木とは1個の光の球体にほかならない.
コラッツ木を「光の球体」とみなす見方はコラッツ木を「ブラックホール」とする見方とは真逆の解釈である.コラッツ光球体の顕著な特性は,球体内部から放射される光線のどの2本も交差することがないという点にある.果たしてそのようなことが可能なのだろうか?ここからストレートに「量子論的な世界」に踏み込むというのもやや無謀であり,明らかに本論の範囲を超えるものである…
ログを日付順に読むと,コラッツ核木→コラッツ放射高速路系→コラッツ仮想木→銀河高速道路系のような展開になっている.銀河高速道路系では一般コラッツ木を一般道路として位置付け,それと並行する幹線路として仮想コラッツ木を対置している.この比喩は一般道路から高速路への乗り換えなどの連想が効くので理解し易いのではないかと考えた.
2月6日のログには「有効ノード率というのは,最大枝数と樹高を同じ値に設定したときの仮想木と一般木のノード数の比率を表すものでこの値が3/4に収束することは間違いないように思われる.」という記述が見える.この値は「コラッツ数と奇数全体の比率」を表すものであると考えられるとしている.
2月20日付けで「完全正則コラッツ木を構成するためのもう一つの方法」という提案が出てくる.「もう一つの方法というのは至って単純なもので「3の倍数ノードを一律除去する」というだけだ」というのだが…この方法の利点は「3よりも大きい素数が必ず含まれる」という点だ.「3の倍数ノードを除去したコラッツ木には一般道路と高速路という区別は存在しない」ため,「コラッツ銀河高速銀河系」というイメージは放棄され,「仮想木」という概念も破棄される.ここで「コラッツ放射線道路系」というイメージが浮上してくる.このイメージは上記の「コラッツ放射高速路系」に類似しているが,同じではない.
ここで初めて,「コラッツ完全正則木」という概念が確立したと言ってよいのではないか?この時点では別名として「コラッツ中核木」というネーミングが提案されている.ここではコラッツ中核木=3倍数を含まないコラッツ木ということになっている.A面のオプションが「Core tree」となっているのは,この構想を反映している.2月22日に初めて「コラッツ完全木検定」という「製品名」が出てくる.
3倍数は木の終端にしか現れないので,アドレスコードをアレンジしてアドレスコードの末尾に3倍数ノードを付加するような形式に拡張することができる.たとえば,1.2.3.4.5-6で親ノードの6番目の3倍数というポジションを表記できる.もう一つのコード形式として1.2.3.4.5.-6というのも考えられる.負のコードは3倍数であることを示すものだ.これでコラッツ木上の位置を地番として表記できるようになる.英語では地番を lot number ないし parcel number という.parcelは小包という意味だ.郵便番号やIPアドレスなどとも共通する.
これをさらに拡張して偶数を含むすべての整数にアドレスコードを付与することが考えられる.たとえば,1.2.3+4とすればよい.⇒最終的には1.2.3*4で偶数を表記するようになった.これを「詳細付番」と呼んでいる.詳細付番には,a-b, a*b, a-b*cの3種のパターンがある.これですべての整数にユニークな地番を付すためのユニバーサル・アドレス・コードシステムが確立した.実装はすでに完了している.