なぜだろう?また軌跡の描線が出なくなっている.アニメには出力されている.このサンプルでは例外は発生していない.昨日は完全に動作確認したつもりだったのだが…
ポイントは描画できているのに線分が描けないというのはどういうことだろう?2024-03-28-1 では出ている.最新版でまったく同じ設定にしてみたが,やはり動作していない.どうもよく分からないので,ここまで戻ることにする.
いや,それより後の28-2でも動作している.ここまで戻れば十分だ.
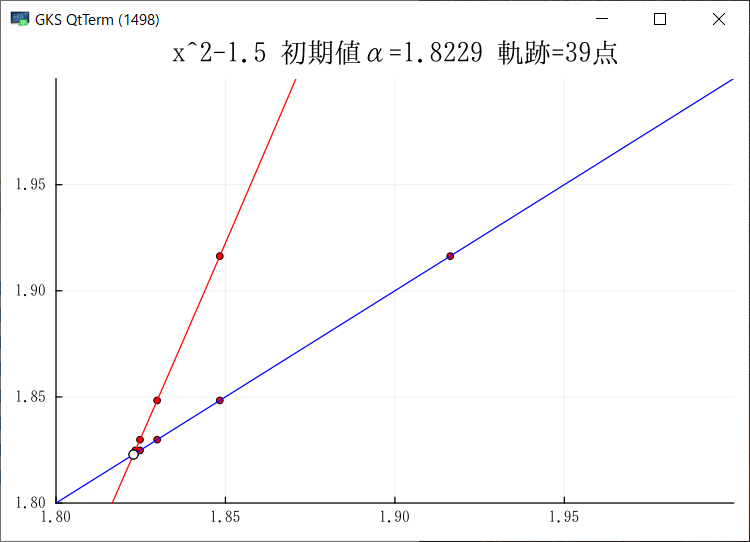
この後,どんな修正が入っているかが問題だ.この版にはすでにRootsは組み込まれていて,Find_zeroで不動点を検出している.実際画面にも描画されている.ここまでできれば立派なものだと思うのだが,何を追加しようとしたのだろう?まず,動線を描画できていないサンプル y=x^2-1.5 初期値α=1.8229を試してみよう.確かに画面には何も出てきていない.
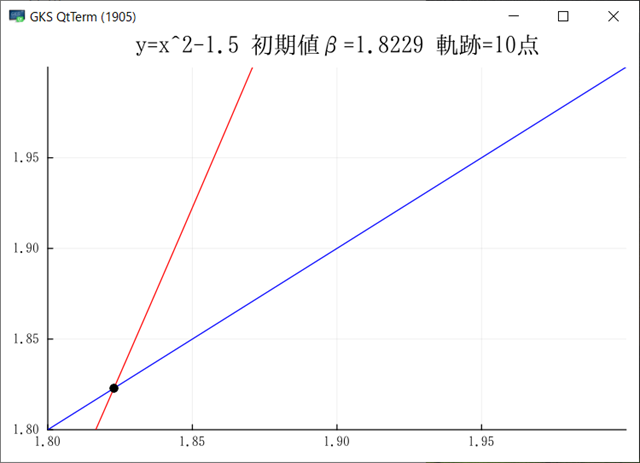
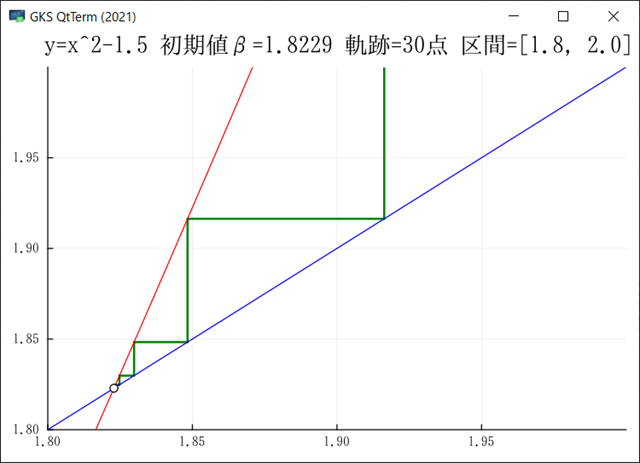
ただし,これは計算や動作が誤っているためではない.開始点=(1+√7)/2 から出発した場合,値の変化が遅くて不動点の◯の外に出られないためだ.これを区間[1.8, 2.0] point:30で描画すると,以下が出力される.
ただし,ステップを増やして,point=34を超えると動線は消えてしまう.
1: 1.82287565553229535809
2: 1.82287565553229552433
3: 1.82287565553229613042
︙
27: 1.84833257470943420165
28: 1.91633330673200616455
29: 2.17233334249042522319
30: 3.21903215089562309242
31: 8.86216798849970155839
32: 77.03802145638884645281
33: 5933.35674991502828268578
34: 35204720.82176222747503632359
35: 1239372368138217.42496308002819849062
36: 1536043866904533138569813670805.66483330243742956258
37: 2359430761055031115005960802378927230275224692180453704350907.12176434601263055879
38: 5566913516212723332117413654604965054786240836971452633864047785437413116991185624735519798218699259766451175951693774848.00000000000000000000
39: 30990526096991907041511225161593806680067925799018141776028714401452471138227479974234438992180424796522079841327601952168724719696008595440015069056256081311447418248647170548763107745965205691210096638929522670926745027633952745003478417408.00000000000000000000
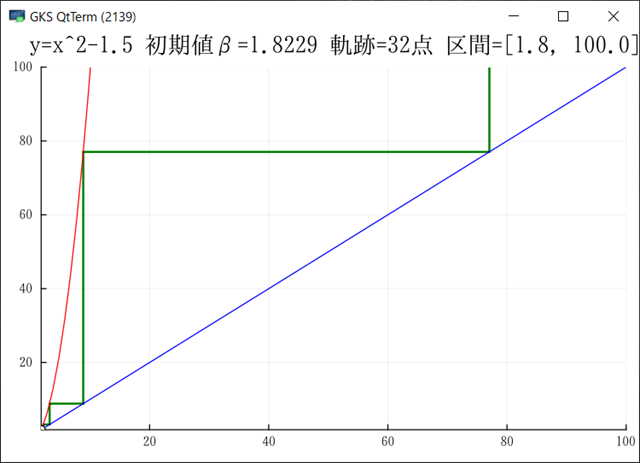
のように変化するとき,39点目で例外が発生しているが,それよりも手前の35点目で描画上の問題が発生するものと考えられる.例外が発生した場合には,例外の発生点から先を切り捨てて自動再計算するようになっているが,動線を描画するためには,maxloopを68以下に設定する必要がある.下図では区間を[1.8-100.0]まで拡大して32点までを描画している.
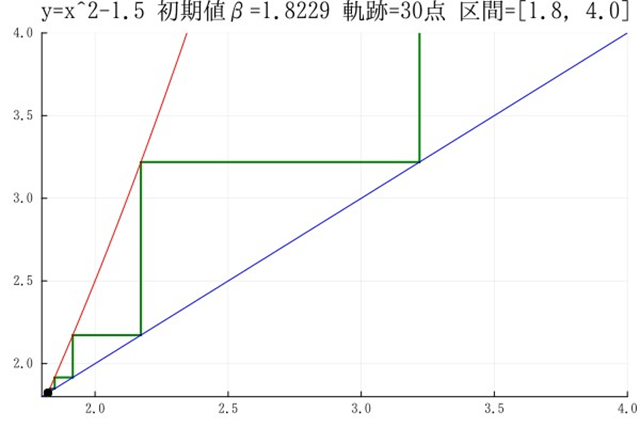
いずれにしても,軌跡の動点数を調整しないと動線を描くことはできないということが分かった.ここで一度バックアップを取ってから,もう少し整理することにしよう.⇒配列XaとYaは廃止できるはずだ.⇒廃止した.⇒lastpos はループの中では更新せず,最後のsweetposから取り出すというのでよいのではないか?(正確に言うと,この点は描画されていない可能性はあるが…)この図は区間[1.8, 4.0]だが,稲妻型の発散としてはこのくらいが分かり易いのではないか?
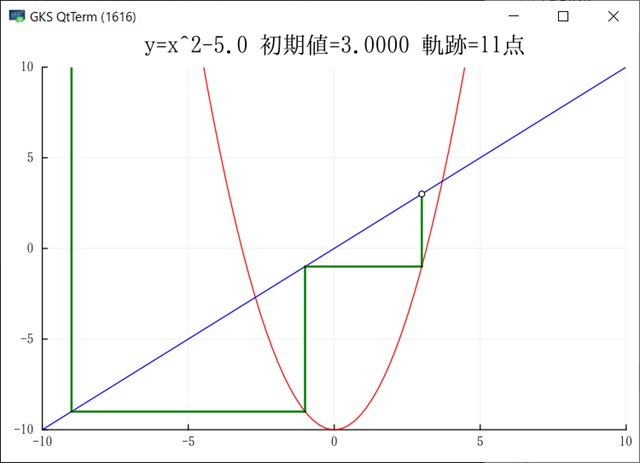
とりあえず,一旦バックアップを取っておこう.ある程度整理が付いた.稲妻型の収束例として以下をピックアップしておこう.
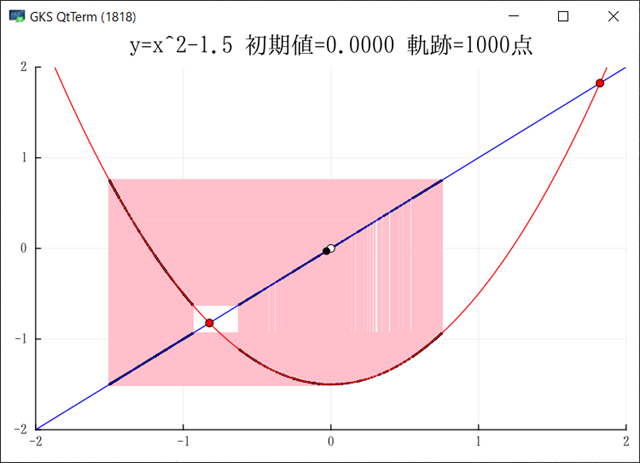
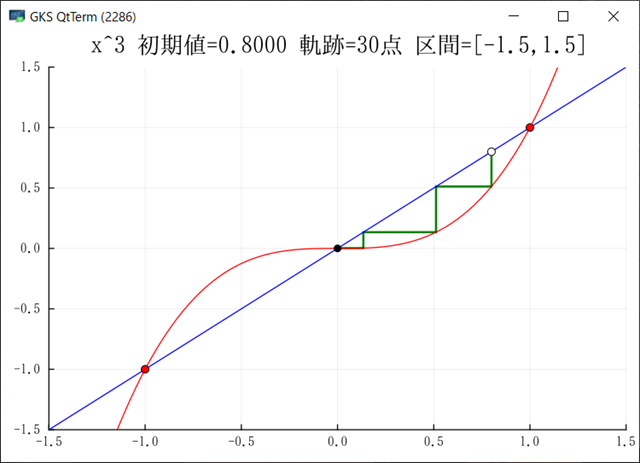
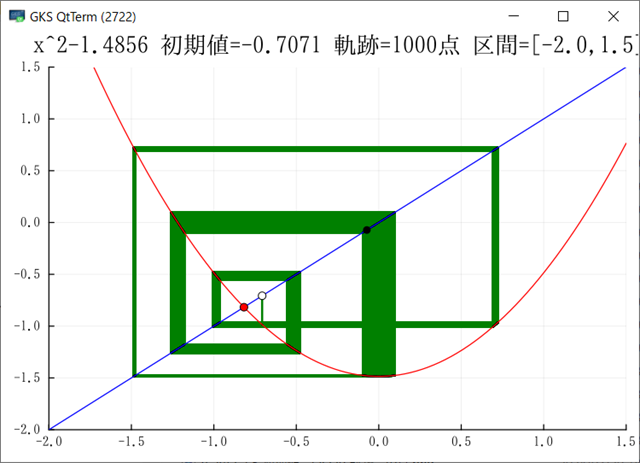
スパイラル型の収束例が欲しい.これがスパイラルではないか?
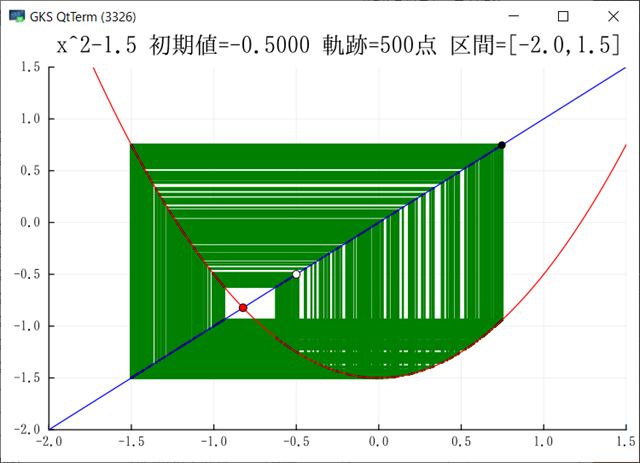
そんな感じだ.通常のメルストロム型とはかなり違う.初期値0.5でもほとんど図柄は変わらない.しかし,x^2-1.5の標準図とは大きな違いだ.下図↓