厄介な問題が出てきた.パネルに出しているαR,γRとマトリックス上のデータが一致しない.原因ははっきりしている.横数列の周期がΘではなく,Θ-1になっているためだ.Θ-1というより,正確に言えばφ(Θ)だ.φ(Θ)の剰余を表示するようにすれば正しく対応できるようになるとは思われるが,そうなると,大きなマトリックスを出す意味が失われてしまう.考えられる方法としては,列ヘッダを2行にして①γの生値と②γ mod φ(Θ) を併記することではないだろうか?そうすると,実際のデータは3行目から始まることになる.
同様のことは行ヘッダに付いても言えるかもしれない.行ヘッダに数字を表示できるようにするにはどうすればよいのか?
https://dobon.net/vb/dotnet/datagridview/drawrownumber.html
①CallPaintingイベントハンドラを使う,②RowPostPaintイベントハンドラを使う,
https://atmarkit.itmedia.co.jp/fdotnet/dotnettips/506dgvlinenum/dgvlinenum.html
https://atmarkit.itmedia.co.jp/ait/articles/0610/27/news141.html
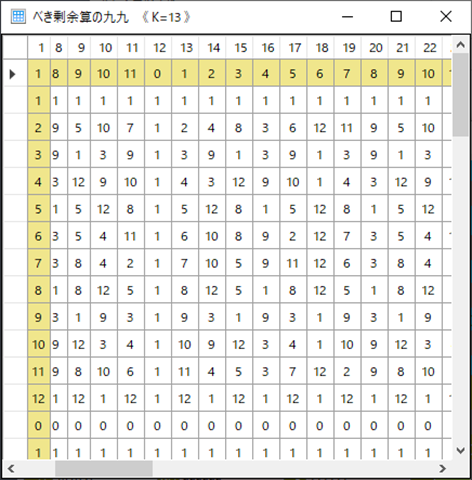
列ヘッダにはγ値が表示されているので,その下の行に γ mod φ(Θ)を出すようにしてみよう.⇒わかり易くなった.この行だけ色付けしてみよう.行ヘッダに関しては現状のままでよい.こんな感じになった.これなら間違いないだろう.この値はγRに対応しているので,γRのテキストボックスの色もグレーにしておこう.
いや,逆にパネルの色に合わせて行をカーキで塗りつぶしてみよう.少し派手めだが,この程度露骨な方がわかり易いと思う.この行を固定できるとさらによいのだが… ⇒やり方はある.Frozenという属性をTrueにすればよい.最左の第一列も同じ色で塗り潰しておこう.完璧だ.
これでマトリックスとパネルを完全に結びつけることができた.あとは行ヘッダを出すだけだ.⇒出た!
.RowHeadersVisible = True
.RowHeadersWidthSizeMode =
DataGridViewRowHeadersWidthSizeMode.AutoSizeToAllHeaders
しかし,セル幅がムダに広くなっている.⇒どうもかなり具合が悪い.
.RowHeadersWidthSizeMode = DataGridViewRowHeadersWidthSizeMode.AutoSizeToFirstHeader
という設定が取り敢えず,一番まともに近いものになるが,二桁以上の数字になると一部が掛けてしまう.AutoSizeToAllHeadersとすればこのようなことは避けられるが,今度は列ヘッダを選択しても列選択できなくなる.これは行ヘッダ幅とテーブルの左上セルの幅が一致しなくなるためだ.⇒多少見苦しいところは残るが,いまのところ,AutoSizeToFirstHeader よりましな方法がない.
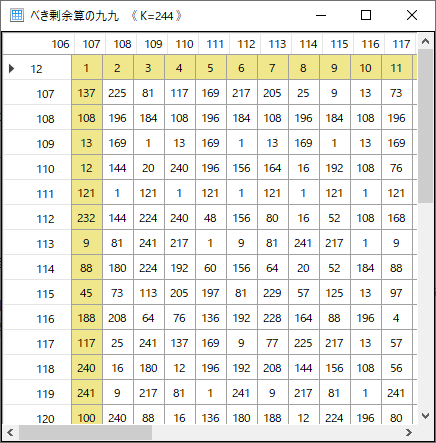
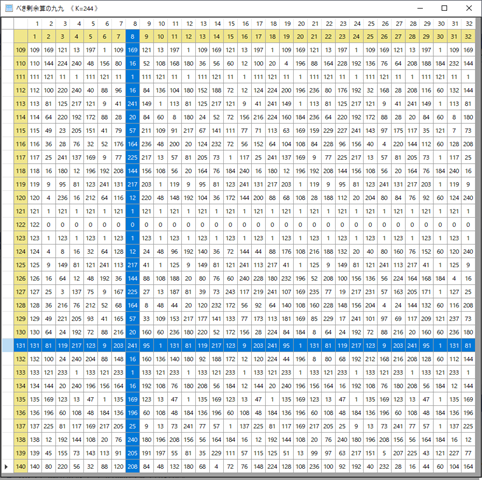
行ヘッダにはマトリックスに表示された範囲の整数値を生で表示したいと思っているのだが,問題がある.マトリックスというのはΘだけで決定されるものであり,α値の如何に依らない.これはγ値についても言えることだが,γ値はすべての検定で1から始まる値なので,特に断らなくてもよいように思われる.テーブルの位置決めにはαRとγRが参照されているので,まるきり無関係という訳ではないが,αやγnは剰余であり,生値は参照されていない.⇒行ヘッダはむしろ非表示という方が分かり易いのではないだろうか?現行では下図のようになっている.
これはΘ=244のマトリックスで,αR=123,γR=122だ.これで見ると,マトリックスの左上点は(107,106)ということになるから生値ではないが,シフトした値が出ていることは間違いない.ただし,どうもまだ正しく動作しているようには見えない.どうもマトリックスの計算が間違っているようだ.α=119,γ=121,Θ=244のとき,R=119のはずだが,マトリックス上にこの値が見当たらない.α=119,γ=96,Θ=89のとき,αR=30,γR=33,R=52はマトリックス上にある.マトリックスの左上点が(1,1)の場合は動作しているのではないだろうか?
いずれにしても行番号をヘッダ部に表示することは諦めた方がよい.むしろ,列ヘッダと同様にヘッダ用の列を別途追加するようにした方がよい.その方が安全だ.
▲行選択→列選択のとき,行選択を解除しないで十文字に選択できるとよいのだが… 列ヘッダでなくコントロールキーを押しながらドラッグして拡張選択する方法で十文字に選択することはできる.またシフトキーを押しながら先頭行のセルを選択すると矩形領域が選択され,その右下セルがRの位置になる.⇒列ヘッダをクリックすると列選択モードに切り替わるが,それを廃止して,列ヘッダのクリック→列のセルを拡張選択するようにした方がよい.⇒対応修正した.
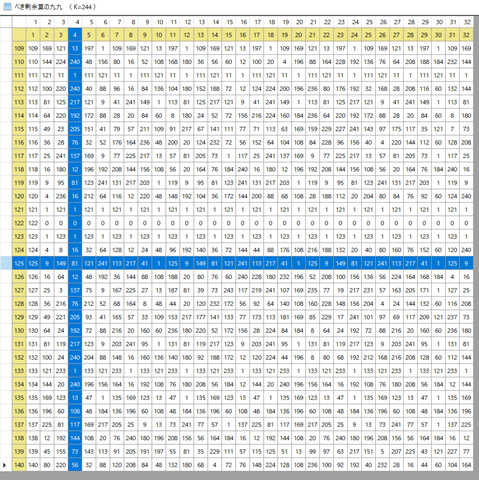
まだ,合わない.α=125,γ=124,Θ=244のとき,αR=125,γR=123でR=149だが,125の行に149という数字は見当たらない.ただし,cycle={125,9,149,81,121,241,113,217,41,1}となっているので,マトリックスの方が間違っているのではないか?マトリックスサイズを36×36から64×64に変えたら乗ってきた.確かにこのテーブルは正しい.⇒γRの値がおかしい.φ(Θ)=120でγRが123というのはあり得ない.⇒以下のような調整を行っている.
If tot < Θ – 1 Then eR = eR + tot
If eR = 0 Then eR = Θ – 1
これが間違っているのではないだろうか?とりあえず,両方止めてみた.今度は一致している.ただし,上記の数字と合っていない.上ではR=149となっているが,R=81だ.正しい答えは81だ.あるいは手順が異なっているのか?テーブルを読み損なっていたか?
列を1個追加してα値を表示するように改修したところだが,この値は実際には剰余を取ってからの値であり,既存マトリックスの第一列目とまったく同じなので表示する意味がない.⇒列ヘッダと同じように通し番号にしてみよう.
この方がよい.この番号はおそらく生値なので巨大数になる可能性もあるが,仕方ないだろう.一応これで仕上がったのではないかと思う.一度バックアップを取っておこう.TestMatrixにも対応しておく必要がある.TestMatrixではマトリックスは生成しないが,テーブルはフルサイズで構築することになっている.当然,左上セルはつねに(1, 1)だ.
▲TestMatrixではダンプは出さない方がよい.時間が掛かり過ぎる.また,カーソルが砂時計にならないのはなぜだろう?⇒テスト完了したら,出力コンソールに何かしらメッセージを出した方がよい.⇒対処した.
▲ダメだ.まだ数字が合っていない.α=125,γ=110,Θ=244,φ(Θ)=120 のとき,αR=125,γR=110 で R=1 のところ,クロスポイントには217とある.cycle={125,9,149,81,121,241,113,217,41,1}なので,R=1 も 217 も候補には入ってくるが… 正しい答えは R=1 だ.ということはγRが間違っていることになる.周期は10でφ(Θ)の約数になっているのだから,φ(Θ)で mod を取るというので間違いないと思われるのだが… γR=94が列の先頭になっている.このときの値は81であっているのだが,その次の数字が217で外れている.つまり,第一列目の選択に問題があるか,ないし,第一列目の評価に問題がある.
周期はそれぞれの行によって異なるので,同期を取るためにはφ(Θ)で分割する必要がある.つねに,φ(Θ)の倍数が第一列に来るようにすればよいのだが,それでは大きなテーブルに対応できない.どうすればよいか?最初の糸口が見つかるまで空回しするしかないのではないか?たとえば,α=125の場合,γ=94ならば,R=81, γ=95ならR=121,96で241,… このマトリックスの値はテーブルから引いているものなので,テーブルが間違っているのだろうか?⇒確かにそのようだ.各項ごとにべきを再計算しなくてはならない.コストは掛かるが仕方ないだろう.
列ヘッダをクリックしてその列を全選択するという操作は簡単に実装できたが,多少使い勝手上の問題がある.単純な拡張選択になっているため,別の列を選択すると複数列が選択状態になってしまう.これはあまり芳しくない.すでに選択されている場合には選択を落とすという動作も考えられるが,この場合の問題はその列全体を落とすと,行選択されている場合に欠落セルが出る可能性がある.現在選択されている行を取り出すことは可能だろうか?SelectedRowsというパラメータはあるようだ.⇒できた.自由に列選択ができるようになった.これで十分だ.
▲αやγに大きい数字を入れると,インデックスが1から始まるようになる.つまり,巻き戻しされてしまう.これでよいのだろうか?⇒マトリックスのインデックス行/列に現れる数値はインデックスであり,生値ではない.つまり,表示されているのはαRとγRであり,それらが見える範囲が表示されているというに過ぎない.従って,これらのヘッダ行ないしヘッダ列にはΘないし,φ(Θ)を超える値が現れることはない.
いや,その説明は間違っている.どちらも通番として表示されているのでΘやφ(Θ)を超えることはある.これは便宜上そうしているだけであって,αやγの生値を表示しているものではないことに注意する必要がある.⇒αやγの数字が大きいか小さいかには関係ない.インデックス行/列に表示されるのは,αRやγRであり,これらの値が小さければ1から始まるようになる.ただし,マトリックスの連続性を強調するために,インデックス行/列に表示される数字そのものの剰余は取らず,通番に見えるように表示している.
▲列ヘッダとインデックス行はまったく同じ内容に見える.列ヘッダは不要なのではないか?あるいは,逆にインデックス行は通番ではなくインデックス表示した方がましかもしれない.その方がわかり易くなると思う.⇒剰余の式が間違っていた.括弧が落ちていた.⇒修正して違いがはっきり見えるようになった.横数列の周期はΦ=φ(Θ)であり,この値はΘよりずっと小さくなる場合もある.γRはこの値を超えない.
▲どうも,まだ合っていないところがある.α=130,γ=115,Θ=244,φ(Θ)=120でαR=130,γR=115,R=172のとき,stripeと縦数列が一致しない.stripeの中に115が出てこない.⇒このリストはGetResidueStripeで生成されているが,ModPowの演算で除数がΘのままになっている.⇒Φに変えてみた.115は出ているが,まだマトリックスと一致しない.⇒stripeに表示されるのはR値であり,当然Θが除数でなくてはならないから,この修正は間違っている.R=172が記載されていないのだから,stripeの誤りと考えられる.
⇒stripeの出力は完全に正しい.マトリックスの読み方が間違っている.インデックス行に表示されている値はインデックスであり,剰余Rではない.つまり,カーキ色の行/列は剰余数列データには含まれない!⇒cycle出力もチェックしておこう.⇒完全に合っている.cycleの桁数はstripeよりずっと小さいが,周期的に繰り返されていることが確認できる.これらのテキスト出力の長さには最大MaxOutput=10000という制限があるが,実用上は特に問題にならないだろう.これでマトリックスは完成したのではないかと思う.