カテゴリー: テント村

前稿（2022/04/06）には，2つの式が記載されている．

ノード番号:=｛長子ノード番号｝.｛兄弟順位｝　　　　　　（１）
長子ノード番号:=｛親ノード番号｝.｛長子識別子｝　　　　（２）

これら２式が正しければ，

ノードN:=｛地番1｝.｛地番2｝.｛地番3｝…｛地番k｝

のようなアドレスコードが可能となり，すべての自然数はその内部にコラッツ木の（暗号化された）アドレスコードを持っているということになると予測される．前稿ではこれら２式について，

『（１）式はNの4進数表記からデコードされ，（２）は3N+1の2進数表記によってデコードされる．3N+1という計算は3進表記した値を1左シフト（した上で1をプラスする，つまり1を右端に連結）することによって得られるから，「演算（代数的操作）」というよりは，「文字列操作」として（形式的に）実行可能であると推定される．』

としているが，果たしてそう言い切れるのだろうか？『（１）式はNの4進数表記からデコードされる』という部分は，3月3日付けのログ「コラッツ国の公用語は４進数である」で説明しているように，ほぼ確実であると言えるが，『（２）は3N+1の2進数表記によってデコードされる』とすれば，以下のような類似問題が成立することが予想される．

拡張コラッツ問題：ｋを任意の奇数（定数）であるとする．任意の自然数Nについて，Nが偶数ならば２で割り，奇数であればｋ倍して１を加える操作を反復すると，かならず１に帰着する

この問題は，Wikiの「コラッツの問題」というページの「類似の問題」という項目に以下のような形式で採り上げられている．

「任意の正の整数 n に対して

• n が偶数の場合、n を 2 で割る
• n が奇数の場合、n に 2m – 1 (m ≥ 1)をかけて 1 を足す

という操作を繰り返すと、有限回で 1 に到達する」

m=1の場合，この命題が成立することは容易に示すことができる．m=2の場合がコラッツ問題だが，m=3の場合，つまりk=5の場合には

13→ 66→ 33→ 166→ 83→ 416→ 208→ 104→ 52→ 26→ 13

のような反例が存在し，成立しない．つまり，「拡張コラッツ問題」は一般には成立しない．上記数列から偶数を除去すると，

13→ 33→ 83→ 13

これを5進で表示すると，23, 113, 313 となる．これらの数字に左シフト＋１の操作を施すと，

231, 1131, 3131

のような5進数が得られる．これを10進表記すれば，66, 166, 416 だから，確かに循環している．これをどう解釈すればよいのだろう？少なくとも，k=5の場合には，（２）式のようなものは成立していないことは確かだろう．そもそもk>3の場合に，「長子木」のようなものが構成可能であるかどうかは，まったく自明ではない．というか，おそらく，k>3の場合には「長子木」のようなものは存在していないのではないだろうか？逆に言えば，長子木のようなものが構成可能であるのは，k=3の場合に限定されるのではないだろうか？いずれにしても，「長子木とは何か？」ということが追求されなくてはならないだろう．

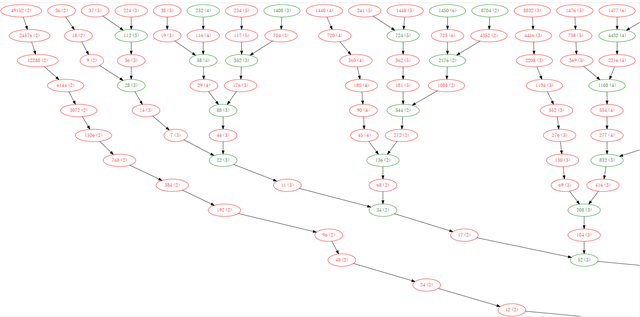
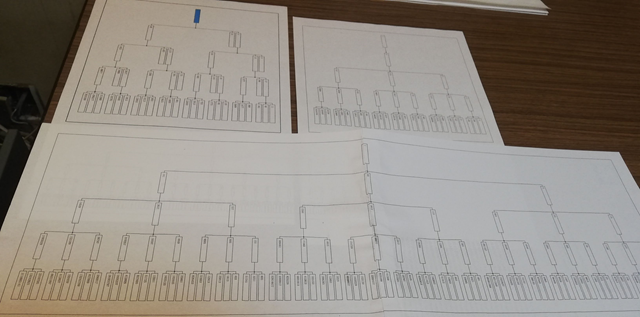
Wikiには「コラッツ予想の他の形式」として，「ボトムアップ方式」という提案が記載されている．「ボトムアップ方式」というのは，いままさに我々がやっている方式そのもので，コラッツ写像の逆演算からボトムアップに木を構成しようとする試みである．この記事では21ステップまでのコラッツグラフのSVG画像↓が紹介されているが，この図版の数値は偶数を含むものであるため，かなり狭い領域しか表示できていない．「完全正則」という概念にも達していないため，証明にはまだほど遠い段階にあり，「予測」の域を脱していない．

拡張コラッツ問題で生成されるようなグラフを拡張コラッツ木ないし，k-コラッツ木と呼ぶことにしよう．上記で見たようにk-コラッツ木は必ずしも「木」にはならないが，そのトポロジーがどのようなものになるのかは興味がある．しかし，ここではこれ以上深入りしないで，先に進むことにする．さて，懸案の仮想木上の拡張アドレスコードに掛かることにしよう．本システムでは偶数は扱わないとしたので，非長子ノード用の書式を追加するだけだ．

区切り文字として「:」を追加する．完全木では区切り文字として，3倍数には「-」を割り当て，2倍数（偶数）を識別するために「*」を追加しているが，「:」と「-」は方式的にはかなり異なる．{x-y}は{x}-{y}であり，「-」で区切られた２つの枝番（XとYは親子関係）だが，{x:y}は全体で１個の一般木上の枝番（x:y）を示している（XとYは兄弟でXはコラッツ数列には表示されない）．

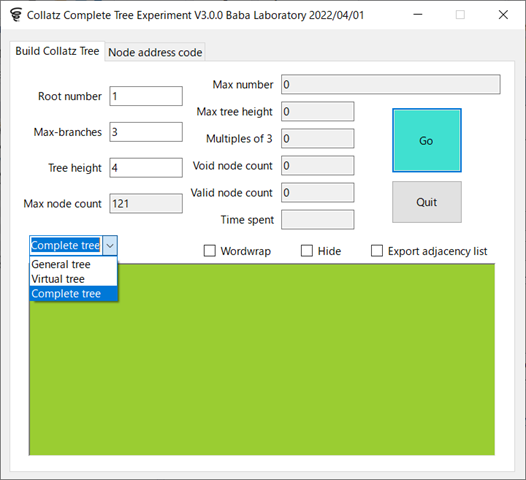
B面ではMax branchesという値を表示している．拡張アドレスの場合はどういうことになるか？仮想木上にないノード（非長子ノード）の枝番は無視するしかないのではないか？というか，長兄ノードは仮想木上にあるので，その枝番を適用でよいと思う．というか，それしか方法がない．幸い非長子ノードはつねに終端に来るので問題ないだろう．⇒とりあえず，アドレス→番号変換は動作するようになった．

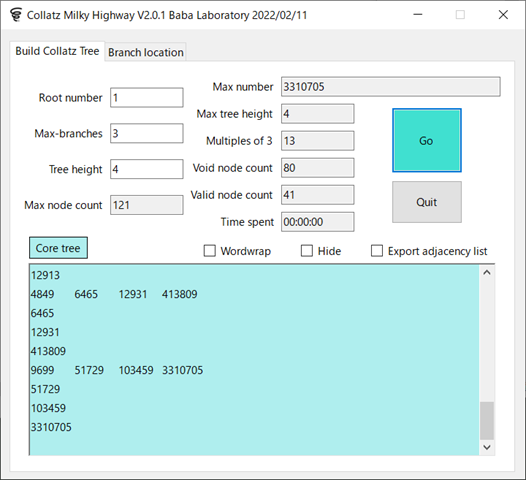
幹線木にも対応修正を入れておこう．幹線木をどう英訳するかでいろいろな候補が挙がっている．①Truncated tree, ②Stem tree，③Minimal regular tree などなど…Nを含む極小な正則木という意味では，③が一番正確であるような気もするのだが…Stem treeでも悪くないような気もする…幹線木というオプションが存在する意義自体がよくわからないという向きには，「極小正則木」という命名は説明になっているような気もする…⇒幹線木も動作している．あとは，コラッツ数列だけだ．

既存コードの出力は，仮想木上の経路だけで止まっている．たとえば，非長子ノードの19397では

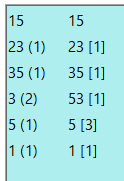
4849    19397
227 (2)    3637 [2]
5 (3)    341 [3]
1 (1)    1 [4]

が出力される．左列が仮想木，右列が一般木だが，左列にはターゲットの19397は表示されていない．19397の仮想木上の経路は1. 3. 2:1で，アドレス変換では

1 [1]
5 [3]
227 (2:1)
19397

のように表示される．これを天地逆転したものが表示されるようにしなくてはならない．つまり，

19397
227 (2:1)
5 [3]
1 [1]

のようにならなくてはならない．⇒大体動作するようになった．

▲幹線木でアドレスに1. 2. 2. 2:1を設定すると，206277の代わりに825109という数字が出てくる．この数字は少なくともダンプ出力の中には見当たらない．successorという変数におかしな値が入ってくる．ループの中で余分なことをやっているようだ．幹線木ではDumpSuccessorsで実行している処理をループ中で重複実行していた．

隣接リストの内容をチェックしておこう．⇒アドレス変換はよいが，他の2つは間違っている．

どうもまだ方針がぐらついている．完全木という構想を捨てて仮想木に絞り込んだ積りだが，完全木には完全木の優位性があり，仮想木にもそれなりの弱点がある．これは結局，「三本桜」という方針が正しかったということを意味するのではないか？というか，どこかでポイントを見失っているのではないだろうか？目標は何か？それをまず確定する必要がある．これまで得られた知見の中でもっとも重要なポイントはノード番号の4進数表記の中には，親から継承したDNAコードと枝番号が埋め込まれているという点だ．これをアドレスコードの流儀で書き下せば，

ノード番号:=｛親から継承したDNA｝.｛枝番号｝

のようになる．つまり，ノード番号は遺伝情報と枝番を「.」によって連結したコード（テキスト）であると言える．親から継承したDNAは長子ノード番号に等しいので，

ノード番号:=｛長子ノード番号｝.｛兄弟順位｝　　　　　　（１）

｛長子ノード番号｝の中には親番号が埋め込まれていると推定されるので，仮にそれが

長子ノード番号:=｛親ノード番号｝.｛長子識別子｝　　　　（２）

のように分解可能であるとすれば，

ノード番号:=｛親ノード番号｝.｛長子識別子｝.｛兄弟順位｝

のように表示可能であることになるから，｛長子識別子｝.｛兄弟順位｝を｛地番｝と置いて，

ノード番号:=｛親ノード番号｝.｛地番｝

のようになり，これを再帰的に展開すれば，

ノードN:=｛地番1｝.｛地番2｝.｛地番3｝…｛地番k｝

のように分節できる可能性がある．つまり，自然数Nをある適切な方法で暗号解読できれば，自然数Nを直接一般コラッツ木上のアドレスコード（ないしそれと等価なある表現形式）に変換できることが期待される．（１）式はNの4進数表記からデコードされ，（２）は3N+1の2進数表記によってデコードされる．3N+1という計算は3進表記した値を1左シフト（した上で1をプラスする，つまり1を右端に連結）することによって得られるから，「演算（代数的操作）」というよりは，「文字列操作」として（形式的に）実行可能であると推定される．このような解析を行う上で有効なフォーメーションとは何か？ということが問題になるが，ともかく，仮想木上で定義された汎用アドレスシステムの実装という仕掛りの作業を片付けておくことにしよう．

以前拡張アドレスコードを実装したときは完全木を対象としていたが，今回の仮想木上のアドレスコードの書式はそれとはやや異なるものになっている．前回の方式では1.2-1というアドレスコードでは

1 [1]→ 5 [2]→ 53 [-1]→ 141

のようなコラッツ数列が出力されていたが，今回方式で{1.2/1}とした場合には，

1 [1]→ 5 [2]→ 113(1)=453

のような動作になる．つまり，5の２番目の長子ノードである113は出力されず，直接非コラッツ数である453が出力されるようになる．既存論理で，453のコラッツ数列を求めると

113    453
5 (2)    85 [2]
1 (1)    1 [3]

が出力され，枝番号リストには{1. 2}が出力されるので，これをアドレス→番号変換すると113という答えが返ってくるため，デュアルな動作になっていない．これはもちろん，{1.2/1}→ 453→ {1.2/1}とならなくてはならない．従って，コラッツ数列取得では

453    453
5 (2/1)    85 [2]
1 (1)    1 [3]

が出力されなくてはならないだろう．この場合，区切り文字の「/」は以前提案されたように「:」とした方が（私の主観だが…）むしろわかり易いかもしれない．つまり，

453    453
5 (2:1)    85 [2]
1 (1)    1 [3]

のようになる．アドレス⇔番号変換ならば，{1.2:1}→ 453→ {1.2:1}となる．この方が読み易いような気がする．また，以前にも示唆しているところだが，本システムでは最終的に「偶数」は扱わないということにしたい．この制限によっても特に不都合が生じることはないと思う…既存コードでCore treeモードで検証テストを実行して出力される隣接リストはかなりあいまいなものになっている．つまり，望むような結果になっていない（と言うより間違っている）．これは上記のような「辻褄の合っていないところ」が存在するためと考えられる．多分，これは上記のようなアドレスコードの導入によって改善されるはずだ．

「三本桜の復活」を止めて，「銀河系の再構築」に方向転換した．一般的なアドレスコードは，コラッツ木のルートノード1からノードNまでの経路上の枝番号の並びを「.」で連結したテキストとして表記される．一般アドレスコードによって任意の自然数のコラッツ木上の位置を一意に決定することが可能だが，このアドレッシングには無効な枝番の並びが生じるという欠点がある．つまり，一般木上では3倍数が終端ノードとなってしまうため，完全正則木を構成することができない．

コラッツ木から3倍数を除去した完全木ではこのようなことが起きないので，完全正則な木を構成できる，つまり，任意のアドレスコードとノード番号に１対１の対応を付けることができるというのが「完全木」を導入した理由である．しかし，3倍数を除去することによって生じるコラッツ木上の空位とアドレスコードの対応は必ずしも自明ではない．仮想木の場合は仮想木上の位置とノード番号の関係は明確に定義されているのでむしろ対処し易いのではないか？と考えられたので急遽方向転換し，汎用アドレスコードを仮想木上で再定義することにした．完全木上のアドレスコードは以下のように定義されていた．

a.b.c….x-y*z　a, b, c, … x, y, z は正の整数

a, b, c…, x は完全木上の枝番を示す1以上の整数で，a.b.c….x のような地番表示によって完全木上の任意のノードの位置を示すことができる．完全木は一般木から3倍数を除去したグラフであり，3倍数の位置を示すためには x-y のような構文が用いられる．これは3倍数Mが親ノードa.b.c….xのy番目の3倍数であることを示している．2倍数（偶数）を表記するためには，y*zの構文を用いる．これは，2倍数Eの親ノードをPとするとき，M=P*2^zの関係が成立することを意味している．完全木上のノードではない数を表記するために使われるx-y*zのような構文を「詳細付番」と呼んでいる．仮想木上のアドレスもこれに準ずる．

1. コラッツ木上で共通の親を持つノードを兄弟ノードとし，兄弟ノードのうち最右に位置するノードを長子ノードとする　長子ノードはコラッツ数と呼ばれることもある
2. 仮想コラッツ木はグラフの連結性を維持しながら，兄弟ノードを長子ノードに合併・縮約することによって得られる一般コラッツ木の簡約グラフである　仮想木上の（1を除く）すべてのノードは長子ノードである
3. コラッツ木上のノードの位置を特定するためのアドレスコードは仮想木をベースとして定義される
4. アドレスコードはルートノード1からノードNに至る経路上で経由する枝番号（兄弟順位）の並びを「.」で連結したテキストである
5. ルートノード1を表記するアドレスコードは空文字列{}である
6. ルートノード1以外の任意のノードNを表記するアドレスコードはつねに”1”で始まる　アドレスコード{1}はノード5を示している
7. 仮想木上に存在しないノード（非コラッツ数）には①非長子（奇数）ノード，②偶数ノードの2種がある　仮想木に非コラッツ数ノードを追加したグラフを拡張コラッツ木とする
8. 非長子ノードUのアドレスは x/y のように表記する ここで，xはUの長兄ノードの枝番号（仮想木），yはUの属する兄弟枠の中の兄弟順位（一般木）である　{x/y}は{x}というパスを含まない　つまり，{x/y}で一つの「拡張木」上の枝番を表示する
9. 偶数ノードEのアドレスは !z のように表記する　ここで，Eの親ノードを奇数Nとするとき，E=N*2^zであるとする　奇数Nはコラッツ数である場合とそうでない場合がある　{!z}で一つの「拡張木」上の枝番を表示する

たとえば，{1.2.3.4/2.!3} は 1[1]→ 5[2]→ 113[3]→ 4835[4]=6601841(2)→ 17604909*2^3→ 140839272 のようになる．コラッツ数列として表示すれば，

140839272→ 17604909→ 6601841→ 4835→ 113→ 5→ 1

である．既存ツールで17604909のコラッツ数列を求めると，以下が出力される．

4401227    17604909
6601841 (1)    6601841 [2]
4835 (4)    4951381 [1]
113 (3)    7253 [6]
5 (2)    85 [4]
1 (1)    1 [3]

この出力では，左列が仮想木，右列が一般木のコラッツ数列となっている．⇒なるほど，確かにこれが仮想木の欠点かもしれない．上記の拡張アドレスコードを使えば，次のような出力になる．

17604909　17604909
6601841 [1]    6601841 [2]
4835 (4)    4951381 [1]
113 (3)    7253 [6]
5 (2)    85 [4]
1 (1)    1 [3]

もし，ここで仮想木ではなく完全木を用いていれば，右列と左列は完全に一致していたはずだ．完全木上には3倍数が存在しないから，3倍数を通過点とするコラッツ経路は存在しない．従って，一般木と完全木はアドレッシングに関しては（3倍数を含めてもほぼ）完全に一致すると考えられる．確かにこれは完全木のかなり大きなアドバンテージであるように思われる．やはり，考察から完全木を（完全に）排除することはできないのではないか？必要なのは，むしろ完全木と仮想木がどのように対応しているかを見ることではないだろうか？それが解明できれば，一般木と仮想木の関係についても自ずから明らかになるのではないか？

「三本桜の復活」というテーマで作業を進めてきたが，ここで大きく方向転換することに決めた．「完全正則木」というアイディアは（少なくとも当面のところ）完全に破棄される．なぜ，「完全正則」というところにそこまでこだわってきたのかと言えば，コラッツ予想問題を解くためにはどうしても，1を出発点としてコラッツ木をボトムアップで構築可能であることを示すことが必要であり，そのためには「完全正則」という縛りが必須であると考えたためであるが，それ自体，ある種の「呪縛」であったと言うこともできる．「仮想木」にはやや変則的なところがあり，「完全正則」から逸脱している部分があるため，それが可能な「完全木」という概念を導入しようとしていたのだが，最終的には「完全正則にこだわる必要はない」という結論に至った．

▲隣接リストをインポートしようとすると，必ず「ライセンスキーの登録」パネルが現れて，キャンセルしても前に進まない．⇒「インポート」機能そのものが，「ライセンス」で保護されているためだ．ゼルコバの木コラッツ特注版はライセンスフリーで公開予定なのでインポートは無条件で可能でなくてはならない．

我々が知ろうとしているのは，「完全正則木」の一般的な性質ではなく，「コラッツ木」という「特殊な木」の性質を調べようとしているのだから，その「木」が「完全正則」でないということを受け入れるしかない．前稿では「長子木」を再定義して，「仮想木」からノード１を除去したものとしている．この再定義は有用である可能性もあるので，一応維持するということにしておこう．つまり，長子木は依然として完全正則木として取り扱うことができる．仮想木とは一般コラッツ木上の兄弟ノードを長子ノードに縮約した簡略木であると考えられるから，仮想木を還元すれば一般木に展開可能であると言えるはずだ．「完全木」に関係するコードをまるごと破棄することになるので，開始プロジェクトはかなり前のバージョンに戻ることになる．

プログラムのタイトルは「コラッツ完全木検定」から「コラッツ仮想木検定」ないし「コラッツ長子木検定」に変わることになる．ここでは一応，Collatz Eldest Sons Tree Experiment というのをプロジェクトの正式名称として採用することにしよう．仮想木検定の最終バージョンを探してみよう．「コラッツ銀河高速道路系プロジェクト」というフォルダにはCollatz Milky Highway V2.0.1 2022/02/11というのが入っている．おそらくこれが最終版ではないかと思われるが，V2.0に入ったばかりなのでもっと新しいものがあるかもしれない．CollatzCoreTreeというフォルダに入っているのはタイトルは上と同じだが，少しだけ新しい．ゼルコバの木のエクスポート機能が廃止され，Virtual TreeがCore treeに変わっている．このCore treeというのは完全木ではなく，仮想木を意味している．ビルド日付は前者が2月20日，後者が2月22日だ．

2月23日にはプロジェクト名がCollatzCompleteに変わっているので，ここで方向転換していることは確かだ．日付入のバックアップではこの他に，CollatzCoreTree 2022-02-22-1というのがある．ビルドの時刻ではこちらの方が新しいので，こちらの方が最新である可能性はある．確かに，バージョンもV2.1.0に変わっているのでこれが最終版と思われる．しかし，オプションのラベルがComplete treeに変わっているので，すでにこの版では完全木に移行しているのかもしれない．いや，内容は変化していないようだ．アドレスコードの区切り文字がコンマからピリオドに変わっているところやボタンラベルがあちこち変わっているなど，新しい構成に移行しつつあることが看て取れる．この版を最新版としてよいのではないだろうか？

ともかく，ここから始めることにする．念のため2月22日頃のログをチェックしておこう．2月22日のログのタイトルは「コラッツ完全木検定と呼ぶことにする」だ．この頃はコラッツ長子木のことを中核木と呼んでいる．いや，少し違う．というより，この版はすでに完全木に移行してしまっている．この記事では「銀河系」と呼んでいるが，そこまで戻らないと抜け出せない．「コラッツ銀河高速道路系プロジェクト」に入っているのはすでに完全木だ．CollatzMilkywayのバックアップは最終が2月12日でかなり古い．いや，もっと新しい版もある．2022/02/20 7:40というのがおそらく最新ではないか？いや，これはすでに完全木に移行してしまっている．⇒ダメだ．頭が完全に混乱している．１→5という単枝しかないのが仮想木だ．もう一度調べ直しだ．

やはり，最初に見たように，2月23日を境目に銀河系から完全木に移行したと見て間違いないようだ．プロジェクト名はCollatzMilkyway→ CollatzCoreTree→ CollatzCompleteのように遷移しているが，CollatzCoreTreeはその過渡期でごく短い期間，多分1,2日しか使われていない．従って，このCollatzCoreTreeというのが，仮想木としての最終版と見てよいと思う．上で採り上げたCollatzCoreTree 2022-02-22-1はすでに完全木に切り替わっている．CollatzCoreTreeというプロジェクト名はほとんど使われていないので，このプロジェクトのフォークという意味で，”CollatzCoreTree”を継承することにしよう．コラッツ完全木検定の最新版はV3.0.0となっているが，このバージョンはここで凍結されるので，新たなバージョンをV3.0.1から始めることにする．

この方向転換はある意味で銀河系に回帰することを意味する．コラッツ銀河系では一般道路を（仮想的に）束ねたものが高速道路であるとしているが，「仮想木は一般木の縮約，一般木は仮想木の展開とみなす」という立場はこれと基本的に等価であり，その関係をより実質的なものとして具体化するのが今回のプロジェクトの目標であると言える．この意味では完全に銀河系路線の継承になっているが，Milky Highwayという名称を用いるかどうか？というところが問題だ．CollatzCoreTreeのアセンブリ名はCollatzCoreTreeになっている…Milky Highwayという名称は結局一度も公式には使われていないので，これを正式名称としてもよいのではないだろうか？タイトルにはMilky Highwayと入っているので，アセンブリ名もそれに倣うことにしよう．

オプションの出力モードにはCore treeが使われている．これは当面そのまま使うことにする．Auto-copy branch ordinal numbersというチェックボックスは廃止する．Export adjacency listはA面と独立にB面でも設定できるようにしておこう．とりあえず，A面はすでに完成しているのではないかと思う．Root numberには2倍数と3倍数は設定できない．いずれも一般木では終端ノードとして扱われているためだ．しかし，仮想木では3倍数は設定できる．これでよいのだろうか？

たとえば，3や75などば3倍数でも仮想木上に存在するが，21や69などは仮想木上のノードではない．21をルートに設定した場合の子ノードは113, 227, 7281などが出現する．これらのノードの親ノードは本来は5なのだが，21という非長子ノードが長子ノードの5の代理人になっているという動作だ．ただし，自ノードより前方にあるノードは21の部分木には現れない．これでよいのか悪いのか，判断に迷うところだが，とりあえず「保留」としておこう．

B面の動作を見てみよう．こちらも特に問題はなさそうだが，汎用アドレスコードには未対応だ．仮想木処理に関してはほぼ現状で完備しているので，今回の修正の本旨は，「仮想木で汎用アドレスコードをサポートすること」にあると言ってよい．それを実現することが，一般木⇔仮想木の対応関係の実装に当たると言えるだろう．

この修正は本来デバッグなしで一発修正で決めるはずだったのだが，結局デバッグになってしまった．あちこちかなり微妙なところがあり，形式論理的なコード操作でカバーできなかった．

▲開始ノードを2に設定してコラッツ数列取得を実行して，IsCollatzNumberで停止する．この関数はNが偶数でないことを仮定している．⇒B面では原則として2倍数・3倍数を含むすべての整数を扱うとしているので，ここで停止するのは不規則動作だ．IsCollatzNumberは仮想木上のノード（長子ノード）をコラッツ数と認定する関数なので，偶数（コラッツ数ではない）は当然偽を返すべきだ．

この関数を呼び出しているGetCollatzNumberはNのコラッツ数つまり長兄ノードを求める関数で，IsCollatzNumberが偽の間はループするようになっているため，この論理では無限ループしてしまう．Nが偶数であるとき，Nの長兄ノードとして何を返せばよいのだろう？標準的なコラッツ木は偶数を含まないので，そもそもNはコラッツ木上に存在していないのではないか？偶数Mが2で割り切れなくなるまで2で除算することで得られる奇数NはMの親なのか？兄弟なのか？

3倍数は一般コラッツ木のノードだが，仮想コラッツ木上に存在する場合もあり，そうでない場合もある．３倍数は完全コラッツ木上には存在しない．3倍数は一般木のノードなので当然親ノードと兄弟ノードを持っている．2倍数は一般コラッツ木のノードではないが，完全木の終端ノードとして表示される場合がある．親ノードは任意の奇数ノードと考えられる．兄弟ノードはこの親ノードPを共有する偶数ノードと考えられる．Pの子ノードである奇数NとPを親とする偶数Mの関係は，言ってみれば異母兄弟のようなものではないだろうか？この意味では異母兄弟の奇数ノードの中の長兄ノードが偶数Mのコラッツ数であると言えないこともない．新版では2のコラッツ数列として以下を出力する．

2
1 [*1]

これは2=1×2^1という計算を表している．１の長子は5である．2と5の間には直接の接続関係は存在しない．もう少し大きい偶数を見てみよう．たとえば，12のコラッツ数列は下記のように表示される．

12
3 [*2]
5 [1]
1 [1]

これで見ると，12の親が3であることは明らかだ．しかし，アドレスコードは以下のように表記されている．

1. 1*2

標準的なアドレスコードは「.」で区切られた正数の並びであるから，上記のアドレスコードは

1.X

のように読まれるべきだろう．Xは詳細付番で1*2という区画を示しているが，完全木上の地番として考えれば，1.1というポイントを示していると考えるのが妥当だ．旧版では2倍数はコラッツ数列取得の対象から除外されているので，偶数が仮想木上でどのような位置を占めているのか（占めるべきか）は分明ではない．仮想木上では一般木上の実親子関係を拡張した「義理の親子関係（養親子関係）」によって木が構成される．つまり，長兄の甥姪ノードはすべて長兄の下に配置される．

話をできるだけシンプルにまとめるとしたら，完全木検定からすべての偶数を排除するというのがむしろ一番わかり易いかもしれない．そうしたからと言って，この論証の正当性はいささかも損なわれることはない．2倍数を含むすべての自然数を表現する汎用アドレスという考え方は魅力的ではあるが，いたずらに問題を難解なものにしているのではないか？アドレッシングという観点から問題をもう一度整理してみよう．

一般コラッツ木は，コラッツ写像（N→N/2，N→3N+1）によって自然に構成されるグラフ（コラッツグラフ）の簡約グラフであり，すべての偶数ノードとそれに隣接する枝を短絡・縮約して得られる奇数ノードのみからなる木である．一般コラッツ木上のノード位置（アドレス）は1からノードNに至る経路上の枝番号の並びによって標識される．一般コラッツ木にはすべての奇数がノードとして含まれる．

仮想コラッツ木は，一般コラッツグラフをさらに簡約したグラフで，同じ親ノードに接続する兄弟ノードはすべて1個の長子ノードに縮約されている．仮想コラッツ木の特徴は（完全）正則木を構成可能であるという点にある．ただし，この正則木にはやや変則的なところがあり，１の直下ノードは5しか存在しないため，厳密には「完全正則木」ではない．仮想コラッツ木はコラッツ数と呼ばれる奇数のみが含まれる．

完全コラッツ木は，一般コラッツ木から３倍数ノードを除去したものであり，完全正則木を構成することができる．汎用コラッツアドレスはこの完全コラッツ木を拡張して３倍数と２倍数を含むようにした「拡張コラッツ木」で定義されるアドレスコードシステムであると言える．完全コラッツ木には3倍数を除くすべての奇数ノードが含まれる．拡張コラッツ木には2倍数・3倍数を含むすべての自然数が含まれる．汎用コラッツアドレスで用いられる枝番号には，2倍数のみをカウントする系統，3倍数のみをカウントする系統とそれらを除外した正準系統の別がある．

新版（完全木）と旧版（完全木）を合体させるという作業を行っているところだが，そのいずれでもないもう一つのバージョンが存在する．タイトルはCollatz Complete Tree Experiment V2.2.0 2033/02/23というバージョンだ．この版はすでに完全木に統一された版になっているが，B面のオプションはOdd numbersではなく，Complete treeとなっていて，この版ではB面でも奇数・偶数の別なく処理することができる．Odd numbersの方が新しいはずだが，むしろデグレードしているような気がする．もう一度開始プロジェクトを調べ直した方がよい．

この版はCollatzComplete 2022-02-24-1というものだ．この後のCollatzComplete 2022-02-25になると，Complete treeというオプションが消えて，Odd numbersに変わっている．⇒この版を取り分けて，CollatzCompleTeとした．もう一度，ここから出直すことにする．この版で12のコラッツ数列を出力すると，一般木では

12
3 [*2]
5 [1]
1 [1]

のように出力され，完全木では

12
3 [*2]
5 [-1]
1 [1]

のようになる．このサンプルには2倍数と3倍数が出てくるので試すのに都合がよい．この版では仮想木のコラッツ数列は取れないが，旧版で3をテストすると，

3      3
5 (1)    5 [1]
1 (1)    1 [1]

のようになる．従って，12から始まる仮想経路は

12
3(*2)
5 (1)
1 (1)

となればよいのではないだろうか？

▲一般木，仮想木，完全木の構成の違いを見るために，印刷しようと思ったのだが，印刷機能が未サポートの状態になっている．横書きサポートに入った時点で止めてしまっている．サンプルファイルは作ってあるが，印刷できない．古いバージョンで印刷は可能と思われるが，横書きがサポートされていない．PageLayoutという関数を復活させれば多分動作可能と思われるが，横書き対応の修正が必要になるので，動くようになるまではかなりの時間を要する．⇒とりあえず，ないよりはましと思われるので，縦書きでプリントしておこう．

確かに，現物が目の前にあるとかなりわかり易くなり，何が問題なのかも把握できる．何をやろうとしているのか？

1. 3種のコラッツ木があり，それぞれが固有のアドレス方式を持っている
2. 3種のコラッツ木にはそれぞれ収容するノードの範囲がある
3. 一般木にはすべての奇数ノードが入っている　つまり，一般木ではすべての奇数ノードに「実アドレス」を与えることができる
4. 仮想木には「長子ノード」だけが入っている　「非長子ノード」のアドレスは未定義と考えられる
5. 完全木には3倍数ノードは入っていないが，別枠のアドレスコード（詳細付番）で位置を特定できる
6. アドレシングの基準は仮想木であると考えられるが，仮想木に載っていないかなりの数の「非コラッツ数（非長子ノード）」がある
7. 偶数ノードは上位奇数ノードに詳細付番を付加して位置を特定する

やはり，偶数ノードは一度システムから省いて考えた方がよいのではないだろうか？偶数ノードを除外すると，特殊ノードというのは長子ノードと3倍数だけになる．仮想木というのは一般木の縮約グラフであり，アドレスの基点がつねに長子ノードにあるという点からすれば，基準コラッツ木と呼んでも差し支えないと思われるが，むしろ，一般コラッツ木から拡張コラッツ木に展開するというのが本筋なのではないだろうか？「コラッツ定理」を証明するためには，「完全正則木」を構成することが必要不可欠と考えられるが，拡張コラッツ木を「拡張正則木」として再構成することも考えられる．

これとは逆に，仮想木を拡張するということも考えられる．仮想木はルート１を除去して５をルートとする木としてみれば，容易に完全正則木を構成可能であり，長子ノードがアドレスの基点になっていることが確かであるとすれば，これはむしろコラッツ木の基準座標系のようなものになっているのではないか？上記項目4で「非長子ノードのアドレスは未定義」としているが，仮想木上に現れない非コラッツ数に付番を与えて位置を特定することは可能なのではないか？

今後は仮想木から1を除去したグラフを「長子木」と呼ぶことにしてみよう．長子木はすべて一般木の長子ノードのみから構成される木であり，ルートは５であるとする．このグラフには本来１の直下にあった部分木は省かれている．たとえば，21, 85, 341, 1365,…などはすべて５の兄弟ノードだが，長子木上には現れない．これらのノードを5+3のような感じで5と同位にあることを示すことはできるだろう．長子木上のノードをNとすると，その兄弟ノードN+kをF(N, k)とすれば，F(N,k)は以下のような漸化式で表すことができる．

F(N, i+1) = 4 * F(N, i) + 1

長子木は完全正則であり，長子木上のノードNは複数の兄弟ノードを持っているが，これらのノードはすべて義兄弟ノードであり，実兄弟ではない．つまり，長子木ノード上のノードの実兄弟ノード（一般木上の兄弟ノード）はすべて長子木上では非表示になっている．上記の式によってこれらの実兄弟ノードにアクセスすることが可能であるから，長子木はすべての奇数に一意のアドレスを与えることができるだろう．これが本当の拡張コラッツ木なのではないだろうか？もちろん，このグラフがすべての偶数を含むように拡張することは難しくない．

長子ノードと親ノードの算術的関係は明確に定義されているので，長子木上で定義された汎用アドレスコードからそのノード番号を割り出すことは難しくない．また，任意のノード番号が与えられたときに，その番号から長子木上のアドレスコードを生成することも可能であると考えられる．もし，この考察が正しいとすれば，現在取り組んでいる完全コラッツ木という概念は破棄されることになるのではないか？つまり，一般コラッツ木と拡張長子木が並立するという構成になり，三本桜は二本ザクラに縮退することになる．長子木が一般木を縮約したものであるとすれば，一般木はむしろ長子木の拡張ないし展開とみなすこともできる．

上記ではNのk番目の実兄弟をN+kと標識するとしているが，むしろ，N:kのような感じで表記した方がよいかもしれない．この場合はもろにNのk番目の弟という意味になり，トポロジー的にも整合性がよいかもしれない．たとえば，

1. 2. 3:4

は，５→３→35→1507→(((1507*4+1)*4+1)*4+1)*4+1 を表すことになる．このような形式で表示されるNの兄弟ノードがすべてNの親のDNAを継承していることは（多分）容易に示せるはずだ．完全コラッツ木というのも悪いアイディアではないが，どこかで座礁する可能性は高い．それよりも長子木を直接拡張する方向のほうが正しいと思う．再定義された長子木にはコラッツ変換のゴールである1が含まれないというところが「奇妙」なところだが，逆にそれがこの問題の「鍵」なのではないかと思う．「コラッツ完全木検定」はすでにかなり作り込んであるが，まるごと廃棄ということになりそうだ．

A面はすでに修正完了しているので，後はB面に対応するだけだ．B面には4つの処理が入っている．①コラッツ数列生成，②アドレス→整数変換，③幹線木生成，④検証テストだ．それぞれを3モードに対応させるとすると，処理は3×4=12個必要になる．しかし，B面で扱っているコラッツ木はすべて直列のチェーンだけなので，一種に統一することは不可能ではないかもしれない．特殊扱いが必要なノードは偶数と３倍数に限られるが，それらは基本的にチェーンの終端にしか現れないので，汎用的なユニバーサルコードシステムで扱うことができる．

④の検証テストは①と②を組み合わせたものだが，「検証テスト」の趣旨から考えると，偶数まで含むユニバーサルコードシステムでカバーすれば十分であるようにも思われる．幹線木というのは，②で生成されるチェーンに枝葉を追加するだけのものなので，従属的な扱いでよい．しかし，①のコラッツ数列取得のダンプ出力はモードによってかなり違う．たとえば，対象ノード番号に15を指定した場合，最新版（最終版）では以下が出力される．

15という整数は，15→ 23→ 35→ 53→ 5→ 1のようなコラッツ数列を生成するが，23[-1]という表記は，15が3倍数であることを示している． 旧版では同じ15から出発してもかなり異なる結果が出力される．下図で左が一般木，右が仮想木モードの出力だ．

　　

右図の仮想木モード出力の右側の列は，左図の一般木モード出力と完全に同じものが出力されている．つまり，旧版では（仮想木モードのときには）一般木と仮想木の両方の結果が出力されている．一般木上のコラッツ数列と，仮想木上のコラッツ数列にはかなりの相違がある．

一般木：15→ 23→ 35→ 53→ 5→ 1
仮想木：15→ 23→ 35→ 3→ 5→ 1

仮想木では数列上に3倍数が現れるというのがもっとも大きな相違点だ．最新版の完全木出力と旧版の一般木出力は15の枝番が負値になっている点を除けばほぼ一致している．ただし，一般木と仮想木の枝番が終端ノードを除けばつねに一致するとは限らない．完全木の（正の）枝番は3倍数を除外した兄弟ノードの順位になっているからだ．旧版の仮想木モード出力を拡張して，①一般木，②仮想木，③完全木の3種のパターンを併記することが考えられる．これ以外の対処法というのも考えられないので，結論的には，（１）B面ではモードを区別しない，（２）コラッツ数列生成では3種のパターンを併記する，（３）それ以外ではユニバーサルアドレスコードを適用する，とするのが妥当ではないだろうか？

これでよいとすれば，修正はコラッツ数列生成の出力に完全木の列を追加するだけで済む．これなら間違いの発生する余地もないだろう．早速実装に移ることにしよう．修正に掛かる前に，既存画面から「Auto-copy branch ordinal numbers」というオプションを外してしまうことにする．このオプションはコラッツ数列生成時に二次的に生成される分岐枝リストをコピーしてアドレス→整数変換のときに再利用するためのスイッチだが，これまで運用した限りではつねにオンにしたままで一度もオフにしたことはないので，「要らない」ということでよいと思う．その方が仕様が単純になってわかり易い．

旧版では，コラッツ数列生成はGetCoreSequenceとGetTheSequenceに分かれている．GetTheSequenceは一般木のみを扱っているので実質的にGetCoreSequenceに含まれているはずだ．GetCoreSequenceと最新版のGetTheSequenceを組み合わせればよいはずだが… ⇒一応修正は入ったが，仕上がりにはほど遠い．3のコラッツ数列を求めただけで無限ループしてしまう．細部をもう少し詰める必要がある．

過去ログもほぼ読み終わったので，実装に移ることにしよう．「コラッツ三本桜」が，①コラッツ完全木，②コラッツ長子木，③コラッツ一般木の3つからなるとすると，プロジェクトの最終版には①と③が含まれているものと考えられる．いや，A面には完全木(full regular)というオプションがあるが，B面にはそのようなオプションはない．つまり，B面は完全木一色になっているはずだ．B面にはOdd numbersというオプションがあるが，これは検証テスト（Verification）を偶数まで拡張するためのものだ．従って，B面ではコラッツ一般木は扱われていない．

「コラッツ完全木検定」に移行する前のプロジェクト「コラッツ銀河高速道路系」ではA面，B面のどちらにも仮想木(Vertual tree)というオプションがあり，デフォルトでは一般木を出力するようになっていたが，最新版の「コラッツ完全木検定」では「ユニバーサルアドレスコード」を前面に押し出しているので，長子木をベースとするアドレッシングは不用になったものと判断された．しかし，ノード番号の4進数解析などで出てくる「兄弟順位」は長子ノードを基準とするものであり，「ユニバーサルアドレスコード」はむしろ便宜的なコーディングとも言える．

この意味では，「ユニバーサルアドレスコード」ないし，「コラッツアドレスコード」というのは，ちょっと気の利いた「アイディア」，ないし「思い付き」に過ぎない．ただし，このコードを使うとコラッツ木全体にシームレスにアクセスできるという利点もあり，捨て難いところもある．逆に「詳細付番」などやや回りくどい説明が必要になるというデメリットもあるが…A面を最新版，B面を銀河系から取るなどの折衷案も考えられるが，却って混乱の元になるような気もする．やはり，単純に三択できるようにするしかないのではないだろうか？

いずれにしても，ロジックはすべて実装してあるので，それらを継ぎ接ぎしてパッチするだけだ．慎重な作業は必要だが，注意深くやればそれほど難しい作業ではない．ともかくやってみることにしよう．「コラッツ銀河高速道路系プロジェクト」というフォルダがある．これが「旧版」の最終版であることを確認しておこう．この中に入っているExEは2月20日にビルドされたものだ．「完全正則コラッツ木を構成するためのもう一つの方法」というのは2月20日に出てきているので，これが最終版と考えて間違いないだろう．この版はV2.0.2 REL 2022-02-11だ．最新版の方はV2.2.1 REL 2022-02-26となっている．

間違いないようにまず，バージョン番号から変えておくことにしよう．V3.0.3 REL 2022-04-01とする．アセンブリ名もCollatzCompleteTreeに変更しておこう．ビルド後イベントも書き直しておく必要がある．アイコンも変えたいところだが，これは後で考えることにしよう．⇒とりあえず，旧版のVirtual Treeというボタン2個を最終版の画面に追加した．さて，このあとどう調理したらよいか？⇒いや，ボタンではなく，最初からコンボボックスを使って三択できるようにしておこう．選択肢は，①General tree，②Virtual tree，③Complete treeとした．

モードを選択するとボックスの背景色が変わるようにした．A面では一般木と完全木はすでに実装済なので，仮想木処理を追加すれば完成する．GenerateCollatzTreeをトレースして差分だけを挿入するようにしてみよう．処理本体はGetRegularCollatzTreeだ．いや，ここまではまったく同じだ．CollatzTreeStructureで相違点が出てくるのではないか？⇒この関数の内部で場合分けするようにした．無効ノードカウント以外は完全に動作するようになった．この数字はUpdateParameterで更新されている．⇒対処した．これでA面は完全に動作するようになった．

B面は明日ということにしよう．

『コラッツ木からすべての３倍数を除去したグラフをコラッツ完全木，コラッツ完全木上のノードをコラッツ数とする』これがコラッツ完全木の直截な定義だ．いや，まさかそんな単純なものであるとは思わなかった．コラッツ完全木上のすべてのノードNは，

ADR(N) = X1. X2. X3….Xk ：Xi は任意の正数，kも任意の正数

のような任意の長さのアドレスコードで位置を特定することができる．アドレスコードからノード番号を求める関数をADR2NUM(アドレスコード)とすると，コラッツ予想問題を解決するためには，以下のような定理が成立することが必要かつ十分である．

コラッツ定理：アドレス→ノード番号変換関数ADR2NUM(A)は任意のアドレスコードAとコラッツ数Nを１対１に対応させる写像である．ADR2NUMの逆変換をNUM2ADR(N)とすると，NUM2ADRは任意のコラッツ数NからアドレスコードAへの１対１写像である

我々がすでにほぼ出口に差し掛かっていることは明らかだろう．コラッツ木からはあらかじめ偶数つまり，すべての２倍数が省かれている．言い換えれば，コラッツ完全木とは２倍数と３倍数を除去したコラッツグラフであると言える．コラッツ木から２倍数が除去される根拠は任意の偶数Mを2で除する操作を繰り返すことによって，必ずあるユニークな奇数（１を含む）に帰着するという理由による．同様に３倍数Tが除去される根拠は3T+1がつねに偶数になるという理由によると言えるだろうか？

確かにこれは直観的には明らかであるようにも思われるが，根拠としては薄弱である．もし，それが可能であるとすれば，以下のような定理が数学的帰納法によって証明できなくてはならない．（ここでは「コラッツ数」とは１から到達可能なコラッツ経路が存在することとする）

前提：ある任意の素数Pより小さい素数はすべてコラッツ数である
帰結：素数Pより大きい素数で最小のものをP’とするとき，素数P’はコラッツ数である

これを言い換えると，すべての整数を含むコラッツグラフから，2倍数，3倍数，5倍数，7倍数….を除去したグラフは連結であることを証明せよ，ということになる．2倍数および3倍数をグラフから除去してもグラフの連結性には変化がないことは容易に示せるが，それよりも大きい素倍数を除去したときにどうなるかは自明ではない．このことは逆に，偶数と３倍数を含む任意の自然数を標識するアドレスコードシステムが可能であることを示している．実際それが可能であることは「詳細付番」を含むユニバーサルアドレスコードシステムとして確立された．

この「ユニバーサルアドレスコードシステム」を今後はユニバーサルコラッツアドレスコードないし，コラッツアドレスコードと呼ぶことにしよう．上記のコラッツ定理はもちろん，コラッツアドレスコードと（偶数を含む）任意の整数との相互変換について成立しなくてはならない．aを３倍数を除く奇数，ｂを３倍数，eを偶数とするとき，詳細付番には，a-b, a*e, a-b*eの3種のパターンがあり，かつそれ以外のパターン，たとえば，a-b.a’やa*e-bは存在しない．

我々はすでに「コラッツ国の公用語は４進数である」ということを知っている．つまり，「自然数Nの名前を４進数で表記すると，Nの名前の中にはNの親Pの名前と兄弟順位が埋め込まれている」ことを示すことができる．しかし，ここで一つ問題が発生する．「コラッツアドレスコード」ではコラッツ数の兄弟順位と非コラッツ数つまり，3倍数の兄弟順位を別建てで計算している．おそらく，このことが「三本桜」を復活させようとする試みの動機になっているのではないか？と推定する．まだ過去ログを読み切っていないので，もう少し読み続けることにしよう．

2月26日の記事に，『我々の方法の中でもっとも重要なポイントはやはり「長子ノードの発見」ということにあるのではないだろうか？』とある．これは，ノード番号の16進数表記を解析して，標識の上位ビットが長兄ノードのバイナリ表現，下位ビットが兄弟順序数を示すことを突き止めたあとに書かれたテキストだ．これを受けて，「我々の提案の中には，①一般コラッツ木，②コラッツ長子木，③コラッツ完全木という三種の木構造が含まれているが，これらのうちのどの一つも説明/証明に欠かすことはできないように思われる」と結論付けている．つまり，これが「三本桜復活」の動機である．翌日のタイトルは「山の八合目からの眺望：８進数で眺めると」で，その翌日が「小学校入学記念写真は三本桜の下で撮影する」だった．

ここで問題になるのは，長子ノードのバイナリ表現を親ノードのバイナリ表現に変換する方法だ．ノード番号を16進ではなく4進表記すると，

兄弟ノード番号＝長子ノード番号＋1の並び

のようになる．長子ノード番号は親ノードから引き継いだDNA配列を示していると考えられるが，子ノード番号をNとして，3N+1を2進数表記してやると，この遺伝子コードを解読することができる．つまり，

子ノードNの３N+1バイナリ表現＝親ノードのバイナリ表現＋0の並び

のようになっている．この計算を実行する代わりに3進数表示してみたらどうなるか？というのが興味の焦点だ．この実験を行うためにはやはり，長子木を任意に出力できる仕掛けが必要になってくる．この辺りは，3月3日の「コラッツ国の公用語は４進数である」にまとめられている．ここで企図した実験を効率的に実施するために，ゼルコバの木の「横書き」機能拡張が導入された．横書き機能はほぼ実装を完了したが，まだ少しバグが残っているようにも思われる．これを完全に潰してから「三本桜」に進むのが順当だろう．

未公開だが，コラッツ木ジェネレータ最終版のタイトルは，Collatz Complete Tree Experiment（コラッツ完全木検定）となっている．「完全木」とは「完全正則木」を略したもので，英訳すれば Full regular tree になる．正則グラフとはグラフのすべてのノードの次数（隣接する頂点数）が等しいものを言う．有限木の場合には必ず次数1の終端ノードを持つから正則木というときには，「終端ノードを除き」という追加規定が入る．ただし，完全正則木と言うときには終端ノードは木の最下層（最上階）にしか現れないものと仮定する．一般コラッツ木では3倍数が木の各所に現れるので，完全正則にはならない．

どうも，開発者であるわたし自身の中で「完全木」と「仮想木」の違いがあいまいなものになってきている．コラッツ仮想木とは，別名「コラッツ長子木」と呼ばれるもので，一般コラッツ木上の親ノードを共有する「兄弟ノード」を最上位の「長子ノード」1点に集約した簡約グラフを意味する．3倍数も長子ノードとなることはあるが，その下には兄弟ノードの子ノードが配置されるので，終端ノードにはならない．この意味では仮想木は完全正則であると言える．

▲コラッツ完全木検定のA面で1-3-4の設定で生成されたコラッツ木のCSVをインポートしようとして，「入力文字列の形式が正しくありません」というエラーになった．

開くファイルを間違えていたかもしれない．生成されたCSVはCollatzTree.C.csvだが，別のファイルを開いていた可能性がある．実際，”CollatzTree.C.csv”は正しく開けた．多分ZEL形式のCSVを開いていたのだろう．デスクトップ上にある，CollatzCore.CSVを開くとこのエラーが出る．CollatzTree.CSVでも同じ．CollatzTree.CSVはこれまで何度もインポートしていたような気がするのだが…テキストエディタで開いてみると確かに，これらはZELの一覧表形式CSVだ．⇒間違え易いのでZEL形式CSVは別のフォルダに移動した．

▲隣接リストCSVをインポートするとき，中間的にZEL形式CSVが生成されている．これは作業用の一時ファイルなので使い終わったら削除しておく必要がある．⇒このファイルは動作確認の意味を含めて温存していたが，「一般的な（順序不定の）隣接リストで正しく動作する」ことが確認されれば削除されるべきだ．

コラッツ完全木と仮想木の相違点がわかった．下図で左が仮想木，右が完全木と称するものだ．どちらも1-3-4という設定で出力したものだが，前者が41点に対し，後者は121点ある．

　　　　　　　

後者は厳密に完全３元木になっているが，前者では１階層目に１個しかノードが存在しない．確かに，これが「仮想木」という構成の特異な点だったのを想い出した．この５というノードの特殊性はコラッツ木を理解する上では重要なポイントであり，おそらくこの点を強調することが，三本桜を復活させる動機の一つになっていたのではないかと思う．ログをもう少し読んでみればその辺の事情もわかってくるだろう．

もう一つの用語として「コラッツ核木」ないし「コラッツ中核木」というのが出てくるが，これはコラッツ長子木の別名と考えられる．つまり，コラッツ仮想木＝コラッツ長子木＝コラッツ中核木と考えられる．いずれかに統一するとすれば，コラッツ長子木というのがもっとも直感的なのではないだろうか？「長子木」は「長子ノード」のみで構成される系図木であるという説明は，「なぜ仮想木と呼ばれるのか？」あるいは，「なぜ中核木なのか？」を説明するよりわかり易いような気がする．「仮想木」と呼んでいるのは，仮想木上のノードを接続する枝が，「コラッツ写像」を直接反映した「実像」になっていないためだ．

「長子ノード」はときに「コラッツ数」と呼ばれることもある．コラッツ数として区分される整数の集合が，コラッツ木の骨格であり，それ以外は葉肉であるというのが「コラッツ中核木」の由来と考えられる．ルートが５であるようなコラッツ中核木（の部分木）を考えると，これは完全正則木を構成可能である．つまり，コラッツ中核木からノード１を除外した部分木は完全正則木の条件を満たしている．

しかし，我々の「コラッツ完全木」はノード１を含んでいる．その構成原理を明示しなくてはならない．⇒その前に「コラッツ放射高速道路系」という概念が登場する．「木」は通常「ルートノード」を根とする樹状の図形として描画されるが，ルートを中心とする放射線路系として描画されてもよい．この意味ではコラッツ木とは１/５を始点として放射線状に投射される交差しない数直線の集合とみなすことができる．

ルート５から投射される放射線は無数にあり，１本の放射線上には無数の点がある．これらの無数の点はそれ自体が放射の中心点となって全方向に無数の放射線を投射している．５をルートとする完全正則木の終端ノードはすべてルート５から等距離にあると考えられるから，これらの集合は１個の３次元的な球面上にあると言える．この放射線を光線とみなせばコラッツ完全正則木とは１個の光の球体にほかならない．

コラッツ木を「光の球体」とみなす見方はコラッツ木を「ブラックホール」とする見方とは真逆の解釈である．コラッツ光球体の顕著な特性は，球体内部から放射される光線のどの２本も交差することがないという点にある．果たしてそのようなことが可能なのだろうか？ここからストレートに「量子論的な世界」に踏み込むというのもやや無謀であり，明らかに本論の範囲を超えるものである…

ログを日付順に読むと，コラッツ核木→コラッツ放射高速路系→コラッツ仮想木→銀河高速道路系のような展開になっている．銀河高速道路系では一般コラッツ木を一般道路として位置付け，それと並行する幹線路として仮想コラッツ木を対置している．この比喩は一般道路から高速路への乗り換えなどの連想が効くので理解し易いのではないかと考えた．

2月6日のログには「有効ノード率というのは，最大枝数と樹高を同じ値に設定したときの仮想木と一般木のノード数の比率を表すものでこの値が3/4に収束することは間違いないように思われる．」という記述が見える．この値は「コラッツ数と奇数全体の比率」を表すものであると考えられるとしている．

2月20日付けで「完全正則コラッツ木を構成するためのもう一つの方法」という提案が出てくる．「もう一つの方法というのは至って単純なもので「3の倍数ノードを一律除去する」というだけだ」というのだが…この方法の利点は「3よりも大きい素数が必ず含まれる」という点だ．「3の倍数ノードを除去したコラッツ木には一般道路と高速路という区別は存在しない」ため，「コラッツ銀河高速銀河系」というイメージは放棄され，「仮想木」という概念も破棄される．ここで「コラッツ放射線道路系」というイメージが浮上してくる．このイメージは上記の「コラッツ放射高速路系」に類似しているが，同じではない．

ここで初めて，「コラッツ完全正則木」という概念が確立したと言ってよいのではないか？この時点では別名として「コラッツ中核木」というネーミングが提案されている．ここではコラッツ中核木＝3倍数を含まないコラッツ木ということになっている．A面のオプションが「Core tree」となっているのは，この構想を反映している．2月22日に初めて「コラッツ完全木検定」という「製品名」が出てくる．

3倍数は木の終端にしか現れないので，アドレスコードをアレンジしてアドレスコードの末尾に3倍数ノードを付加するような形式に拡張することができる．たとえば，1.2.3.4.5-6で親ノードの6番目の3倍数というポジションを表記できる．もう一つのコード形式として1.2.3.4.5.-6というのも考えられる．負のコードは3倍数であることを示すものだ．これでコラッツ木上の位置を地番として表記できるようになる．英語では地番を lot number ないし parcel number という．parcelは小包という意味だ．郵便番号やIPアドレスなどとも共通する．

これをさらに拡張して偶数を含むすべての整数にアドレスコードを付与することが考えられる．たとえば，1.2.3+4とすればよい．⇒最終的には1.2.3*4で偶数を表記するようになった．これを「詳細付番」と呼んでいる．詳細付番には，a-b, a*b, a-b*cの3種のパターンがある．これですべての整数にユニークな地番を付すためのユニバーサル・アドレス・コードシステムが確立した．実装はすでに完了している．

少しだけ歩行距離を伸ばした．スマホを持ち出していないので正確なところはわからないが，3000歩くらいは行ったのではないだろうか？桜も「ほころび始め」どころか，すでに「七分咲き」という感じになっている．「三本桜の実装」に移る前に，これまでの暫定修正をフィックスしておこう．だいぶペースが落ちているが，ぼちぼちと行くことにする．冬物のもこもこスリッパを履き捨てて（と言っても来年もまた履きますが…），夏物に変えた．（去年使っていた）ダイソーのスリッパは流石に作りが悪くあちこち縫い直した（一部はボンドで仮補修）．

一通りフィックス完了した．いよいよ三本桜の復活に進むという段だが，だいぶ離れていたのでカンが鈍くなっている．少しログを読み直しした方がよいと思う．この構想の発端は「ユニバーサルコードシステム」というアイディアがでてきた辺りと思われるので，2月下旬まで遡らなくてはならない．コラッツ木生成ツールの最終ビルド日付は2月26日になっている．マニュアルの更新日付を見てみよう．というか，その前にバックアップを整理して開発履歴が見えるようにしておく必要がある．今回導入した2TBのHDDはそのために購入したものだ．

コラッツプロジェクトには現在3つのバージョンがある．

1. CollatzComplete　最終ビルド：2022/02/26　V2.2.1
2. CollatzCoreTree　最終ビルド：2022/02/22
3. CollatzMilkyway　最終ビルド：2022/02/20

わたしの感覚ではCollatzCoreTreeの方が古いような気がするのだが，違うのだろうか？走らせてみればわかるだろう．CollatzComplete が一番新しいものであることは確かだ．V2.2.1でRel 22/02/26となっている．A面のオプションがFull regularとなっている．つまり，完全正則木を生成するというオプションだが，完全正則でない場合には何を出力するのだろう？⇒少し動かしてみればわかる．Full regularでない場合には3倍数は終端ノードになるが，Full regularの場合にはそうならない，つまり完全正則木が出力される．

CollatzCoreTree はV2.0.1でリリース日付は22/02/11，タイトルはCollatz  Milky Highwayとなっている．この版ではA面のオプションはCore treeとなっている．コラッツ中核木という意味だが…コラッツ中核木では無効ノードが発生しているので，完全正則ではない．1-3-4という設定でビルドしたとき，中核木では有効ノード数41となるのに，中核木オフの場合には46になる．どうも開発者本人すらどういう仕様になっているのかよくわかっていないようだ．

CollatzMilkyway バージョンもV2.0.1 Rel 22/02/11となっていて，CollatzCoreTree とまったく同じだ．ただし，A面のオプションはVirtual Treeとなっている．ただし，名前を付け替えただけで動作的にはまったく同じように見える．タイトルも同じCollatz  Milky Highwayだ．ただし，B面の枝番号数列はコンマ区切りで，CollatzCoreTree になるとそれがピリオド区切りに変化する．ピリオド区切りの方が新しいので，上記リストの順序は妥当なものだろう．

バックアップからマニュアルの原稿を探してみよう．マニュアルの最終版は2022/01/29のCollatzTreeGeneratorManual.pdfのようだ．ownCloudにアクセスしてPDFのバージョンをチェックしてみよう．

ED:1.02 Ver1.1.5 Rel 2022-01-19で確かにこれが最終版と思われる．マニュアルで参照している画像で判断すると，このマニュアルはCollatz Regular Tree Generator V1.1.3 Rel 2022/01/26ということになる．つまり，1月26日以降の修正はマニュアルには反映されていない．少なくともタイトルがCollatz Milky Highwayに変更されたあとの版はまったく未公開ということになる．状況はある程度つかめたような気はするが，ログの読み直しは1月下旬まで遡る必要がありそうだ．

2月17～19日に要対処項目125件というのを拾い出している．これも改めてチェックし直さなくてはならない…1月25日のログのタイトルは「マニュアルはほとんど仕上がった」だ．プログラムの公開版の日付が1月26日となっているので，このころにはプログラムはほとんど仕上がり，マニュアル編集に専念していたものと思われる．併せてかなり長時間のランニングテストを実行している．また，マニュアルの印刷というのも試している．処理速度を計測するためのベンチマークテスト，用語の統一というのも重要なポイントだ．

ZELファイルをダブルクリックで起動してエラーになるという案件がある．ちょっと寄り道になるが，確認しておこう．まず，アプリをインストールする必要がある．

▲最新版ではゼルコバの木フォーマットでエクスポートする機能を廃止して，一般的な隣接リスト出力をゼルコバの木でインポートするという仕様になっている．このとき，隣接リストにはノード番号が記録されているが，インポートした時点でこれを整数範囲内の参照番号に変換（ハッシュ化）している．今のところこれで問題は発生していないが，一般的な（順序不定の）隣接リストで正しく動作するかどうかを調べておく必要がある．

▲CollatzTree 3-5-94.zelのアイコンをダブルクリックしてオープンしたとき，「基準ノード不在」エラーが発生する．描画は可能だが，画面には図面の一部しか表示されていない．データはすべて読み込まれているようだが，再描画しても是正されず，ズーム倍率を変えたりしても一部が切れる現象は残る．⇒いや，倍率100%では完全に描画できた．横書き対応のクリッピングにまだなにか問題が残っているようだ．

最終公開版はV1.1.4 Rel 2022-01-27のようだ．このパッケージを確保しておく必要はある．

▲3倍数が終端ノードとなるコラッツ木で無効ノードカウントを事前に計算する計算式を立てる．（今回の修正が完了するころには容易に書き下ろせるようになっているだろう…）