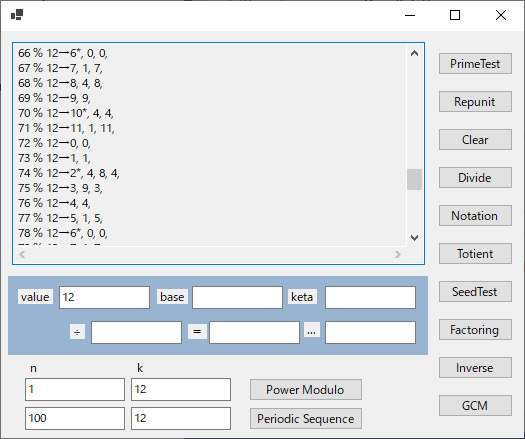
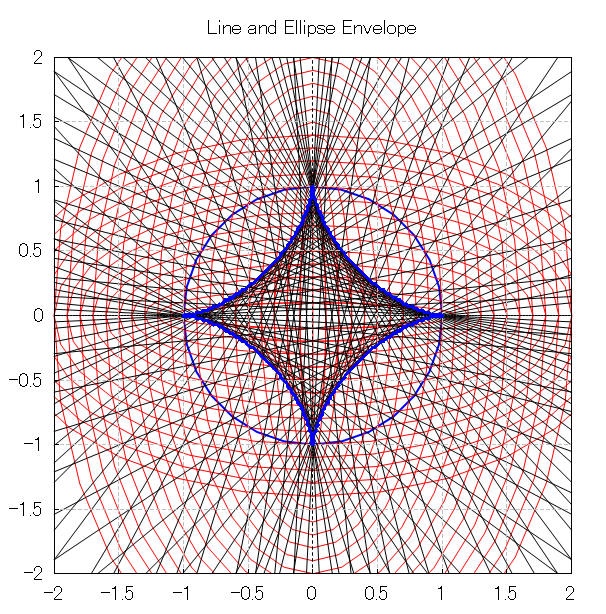
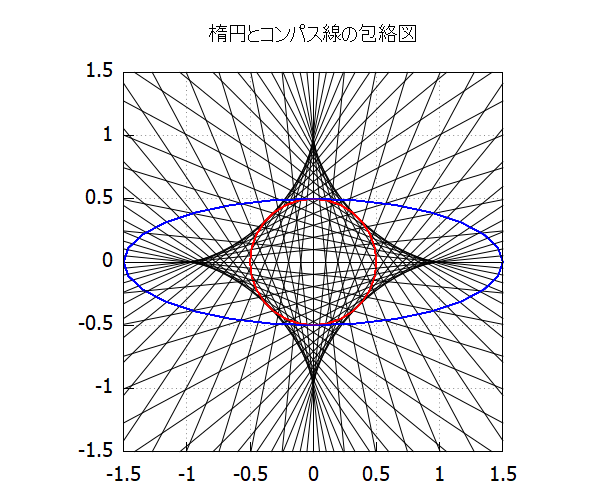
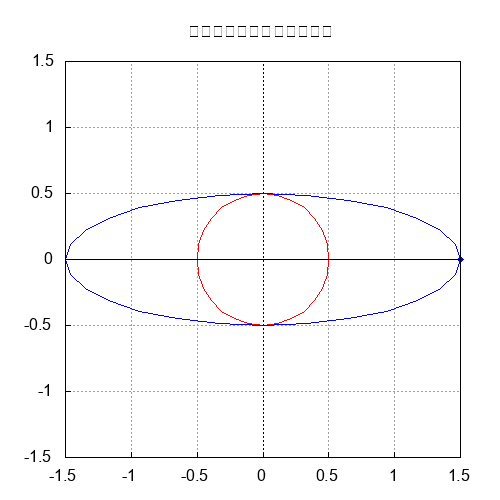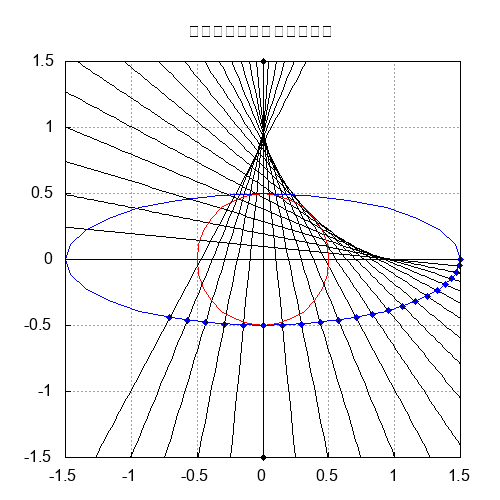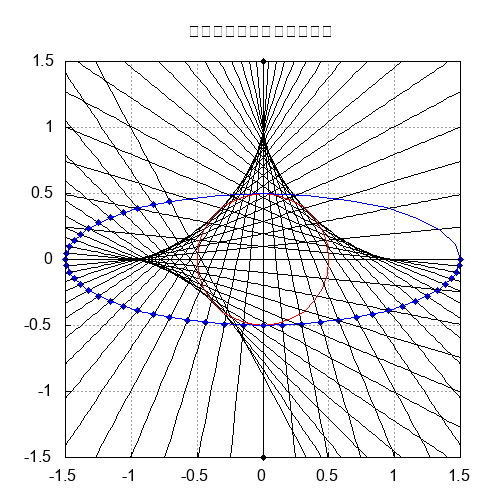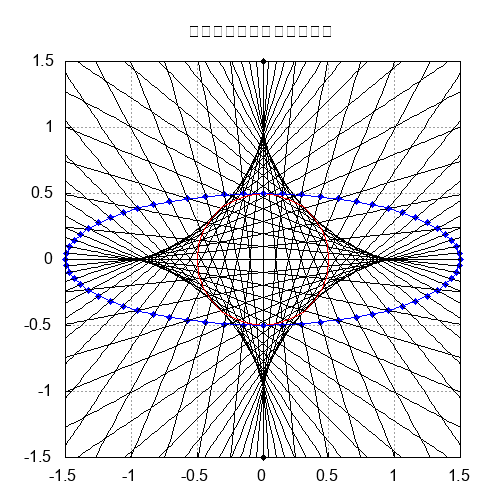
2005年に書いた An Efficient Factoring Algorithm by Repunit Number Method に関係するソースコードを発掘したので,手を入れて動かしてみたい.これはVBで書かれていたもので,VB6を再インストーしてみたが,動作しない.VS2017である程度ファイルを読み込めたので,使えそうな部分だけをコピーして蘇生させてみた.とりあえずなんとか動くようになった.これを仕上げておけば,手元に置くツールとして何かと有用なのではないかと思う.剰余演算や因数分解,φ関数,GCD,単位反復数などが出てくる.使い方の分からないところもあり,よく動いていないところもある.
- Modulo 動作しない
- PrimeTest 動作しない
- Repunit 動作しない
- Division 除算を実行して,商と剰余を出力
- Totient φ(n)を計算しているはずだが,間違っている
- SeedTest エラーが発生する
- Factoring 因数分解のはずだが,何も表示されない
- Inverse エラーになる
- GCM 2数の最大公約数を表示
まず,動作しない機能を動かすところから始めよう.
Moduloは,num0, base, Factorの入力値を取り出して1~Factorまでの剰余数列を画面出力している.これは結局べき剰余でやっていることと同じなので統合してしまうことにしよう.⇒並列動作できるようにしてみたが,両者がやっていることはかなり違う.Moduloの場合は,y*b^p mod k でbは固定,pを1~Factorまで変化させている.つまり n^p mod k で見ると,p^0, p^1, … p^F mod k を出力している.
Modulo では,yが0になると抜けるようになっているので,k=10でb=10の場合は,0を出力しただけで終了してしまう.⇒ようやく,話が合い始めた.結局のところやっていることは同じだ.つまり,ModuloボタンとGoボタンは当機能と言ってよい.Moduloは捨ててよいだろう.
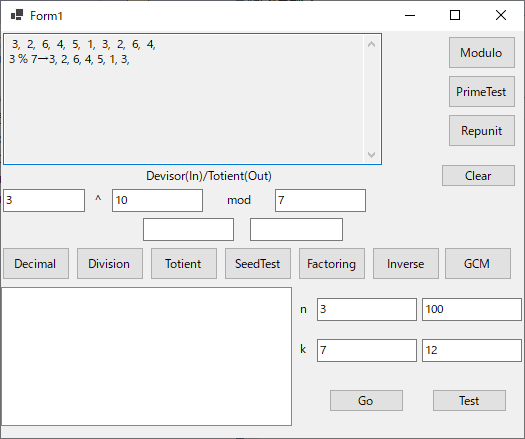
この時期はまだ,周期性というのに気付いていないので,ともかくFで指定した回数だけべきを繰り返すという作りになっているが,現行版ではkで指定した範囲のべきを生成して,その中の一周期分を取り出している.やはり,こちらの方が分かり易いと思う.新版では,nとkの範囲を指定して,n x k のテストを一括実行できるようになっている.一応ここまでできたので,バックアップを取っておこう.⇒失敗した.VSのフォルダで作業していた.開発用ドライブに移動する.
PrimeTest というのがあるが,少し大きそうなので,先にRepunitを見てみよう.これはどういう計算を行っているのだろう?たとえば,22 # 5 → 245411のような数が出力される.入力された b, psi という2つの値から,Σ b^i {i=0→psi-1}という計算をやっている.この値はnum0に入るが,剰余計算では除数(法)に当たる.Decimalというボタンがあって,このボタンを押すと,指定した基数Mで対象数のM進数表記を出力するようになっている.先にこちらを片付けよう.
この機能はアクションとするより,むしろ状態として扱った方がよいのではないか…つまり,たとえば,16進表示を指定すると,画面のすべての数字が16進になるというようなイメージだ.まぁ,そこまでやる必要があるのかないのかもわからないので,とりあえずは,動くようにするというところまでとしておこう.ここで,とりあえず,longを一括bignumberに変換しておこう.⇒BigNumberではなく,BigIntegerだった.⇒定数はBigIntegerにできない.整数除算の\もBigIntegerでは使えない.何を使えばよいのだろう?整数除算はBigInteger.Devide, 乗算はMultiply,BigInteger.Parseなどという関数もある.
quotient = BigInteger.DivRem(dividend, divisor, out remainder)
で,商と余りが同時に取り出せるようだ.^はPowを使わなくてはならない.PowerModという関数が入っているが,これはBigIntegerのModPowと同じものなのではないだろうか?いや,どうも様子が違う.奇数の場合には特殊な操作をしたり,平方してからmodを取ったり… この関数を呼び出しているのは,ModuloMultiとDivideRepunitだ.どりあえず,現行のままBigInteger対応修正だけ入れておこう.BigIntegerでは論理演算はできない.これらに関わる変数は暫定的にLongとしておいた.BigItegerではStrという関数も使えないようだ.⇒Decimalは通常10進と解釈されるので,Notationに改めた.Notationでは16進の場合などアルファベットを使うようにしたいのだが,先に進もう.
Divisionという機能は除算を実行して,商と余りを計算するだけなので,とりあえず現状のままとする.Totientというボタンではφ関数を計算しているが実行時エラーが起きる.Int(n/p)で割り切れているか否かを見ているためだ.この関数は丸ごと差し替えることにする.廃棄する前に比較して動作チェックしておこう.既存関数はLongで動かすようにした.⇒かなり悪い.どうも,PFactorという関数が間違っているようだ.⇒PrimeTableが初期化されていないのではないだろうか?これをやっているのは,Sieveという関数だ.ファイルをロードしたときに実行されている.このテーブルは再定義されるべきではない.Form_Loadイベントが掛かってこないため,sieveが実行されていない.⇒修正した.
MaxPrimeは10^9と定義されているが,実際はその平方根の範囲のテーブルしか作っていない.BigNumberはどこまで大きくなるか分からないので,あらかじめテーブルを作っておくというのは実際的ではない.基本的にPrimeTableを使っている関数は廃止すべきだろう.⇒とりあえず,いましばらく論理だけは置いておこう.⇒Factoringは取り敢えず問題なく動作しているようだ.PrimeTestSubを呼び出して,結果をパネルに出力する.素数の場合には何も出力せず,Factorにそのままの値を書き込む.この処理は取り敢えず不要な気がする.最終的な仕様としては,値を書き込んだ時点で自動実行するようにすべきだろう.
PrimeTestSubという関数は4箇所から呼び出されている.①FactoringClick,②PrimeTestClick,③SeedTestClickx2.Factoringで最後の値を出力しないのはやはり,まずいと思う.たとえば,246をFactoringすると,2,3が出力され,41がFactorに入るが混乱する.やはり,すべての素因数を列挙すべきだろう.となると,1も入れなくてはならない.⇒末尾に「,」が出ないようにする.⇒PrimeTestが動くようになった.verboseというグローバル変数で素因数分解の出力を抑制し,それ以外の付加情報を出力する.
GCMはGCMfuncという自前の関数を使っている.これはaとbのどちらか小さい方yが大きい方xを割り,その余りRを取って,y→x, R→yのように転換してRがゼロになるまでループするというロジックだ.おそらく,これは最速と思われるが,BigIntegerには,GreatestCommonDivisorという関数があるので,今後はこれを使うことにする.SeedTestが動作しないのは,リスト要素が明示的に追加されていないためと思われる.VB6ではこれで動いていたはずなのだが…⇒List1はSeedTestClickで参照されているだけで,内容はパネルに出力されるようになっているから,実質的には不要と思われるので,廃止することにする.
SeedTestClickは内部でPrimeTestSubを呼び出して,その結果を使っている.しかし,画面が乱れるので,PrimeTestSubでは出力させたくない.⇒大体動くようになったのではないかと思う.あとは,数値をチェックして動作を確認するだけだ.一度バックアップを取っておこう
もう一つ機能があった.Inverseというやつだ.これが分からない.⇒それでも一応動いているようだ.n=14のとき,
0, 10
8, 4
3, 4
n=12, K=0, ψ=1, R=0, φ=4, φφ=2
のようなダンプが出る.inverseというのは1/nのことを指している.そして,ここで問題にしているのは,有理数1/nの小数部における「周期列の長さ」である.周期列の長さとは,小数位の桁数のことであるから,その数字列の基数,つまり,x進数という表記形式が決まらなければ決定できない.ψ(b, n) のbはこの意味の基数である.ψ(b, n) はつねにn より小さい.the length y(b,n) of a recursion unit of 1/n is always smaller than n. fixed というパラメータが出てくるが,これは周期性のない固定部の長さのことだろう.この意味では Inverse では,まず,その進数表記に基づいたその数を表示すべきだろう.
Inverse で出てくる商と剰余のリストは何を示しているのだろう?確かにこれは1/nの計算ステップになっている.たとえば,128 base 10の場合は,0.0078125となるが,固定部の長さは7で,Qは{0, 0, 7, 8, 1, 2 5}だ.Rは{10, 100, 104, 16, 32, 64}となっているのだが… この関数の中では対数計算を行っている.pow = log(R) / log(b)という値を計算し,pow=b^powとしている.RTという配列を持っていて,そこにRという値を格納している.xの初期値は1dでそれをnで割る操作を反復しているのだが,x*bを計算して1桁上げてから整数除算を実行しているので,つねにその位の計算が実行されていることになる.
このアルゴリズムでは同じRが出現したときに周期列が完成したと判定し,そこで処理を打ち切ることになる.これはまったく正しいと思う.こういう式が出て来る.
n*U(b,n)=r*(by(b,n) -1)
U(b, n)は recursion unit と呼ばれる数で,rは最初の被除数かつ,最後に現れる剰余とされる.n=21, b=10 の場合,剰余数列は,{1, 10, 16, 13, 4, 19, 1}のようになり,ψ(10, 21)=6,U(10,21)=47619,r=1である.Inverseは大体動くようになったが,まだ動かしていなかったものがある.repunitだ.いや,もしかしたらやってたかな?設定値が欠けていると計算できなくなるようだ.⇒対処した.今度はFactoringが動かなくなっている.あれ,おかしい.動いた.どこを押してたのだろう?いや,やはり何か動作不良なところがある.SeedTestを実行するとおかしくなるような気がする.どこかでout.textを消去する余分な動作が入っているのではないだろうか?ともあれ,かなり整ってきた.