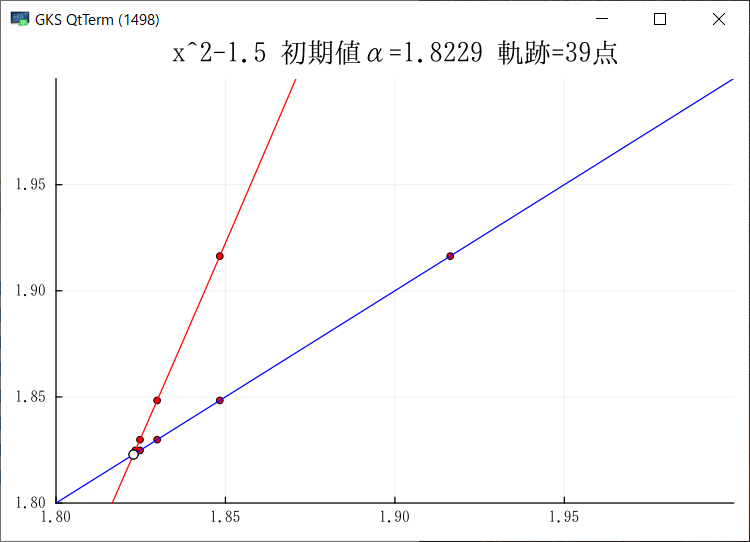
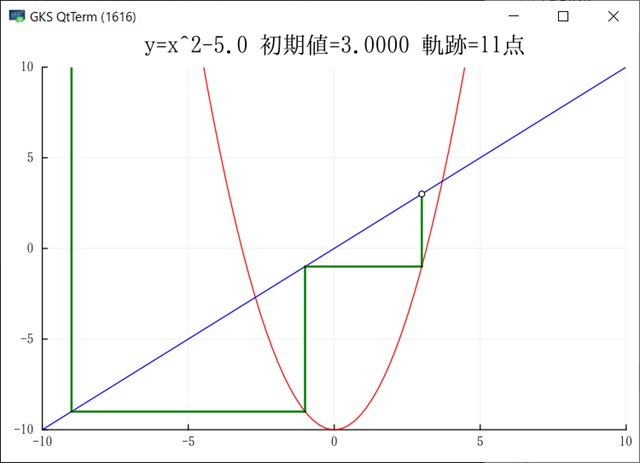
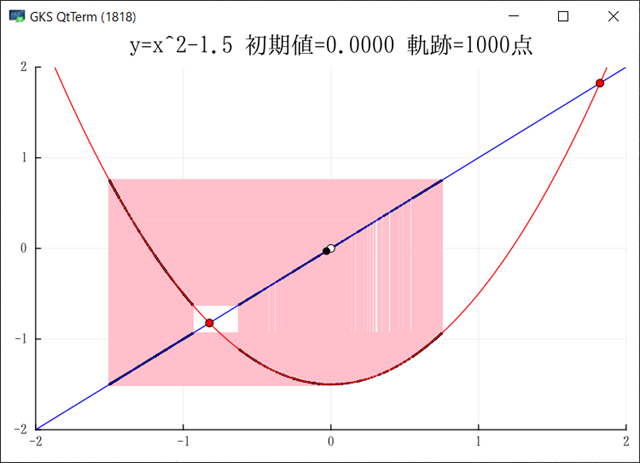
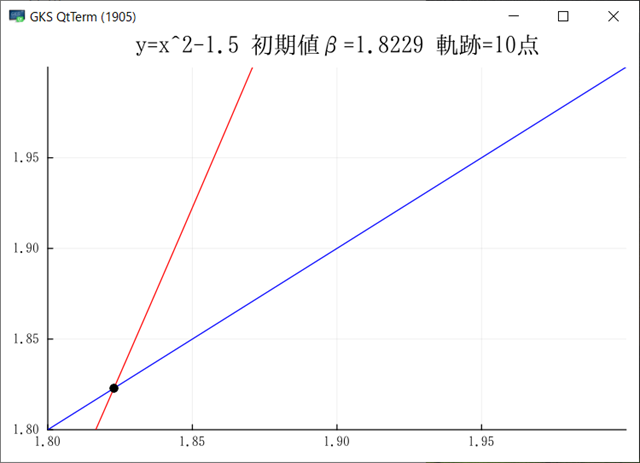
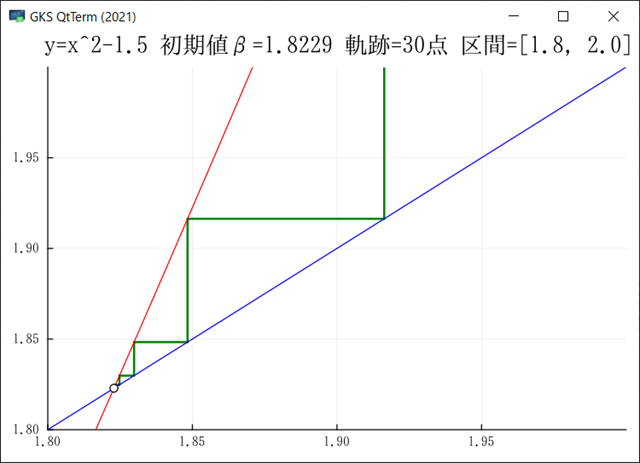
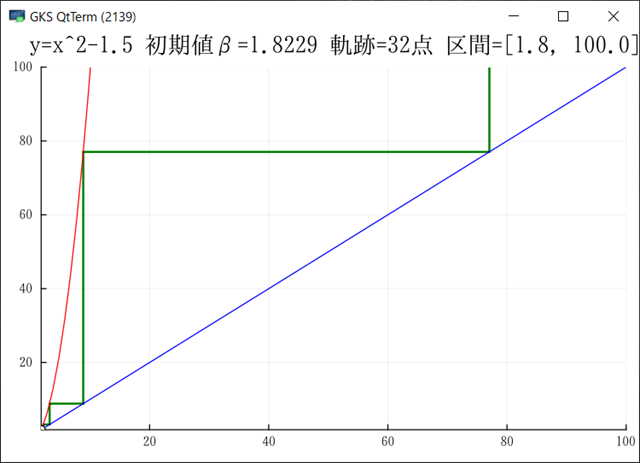
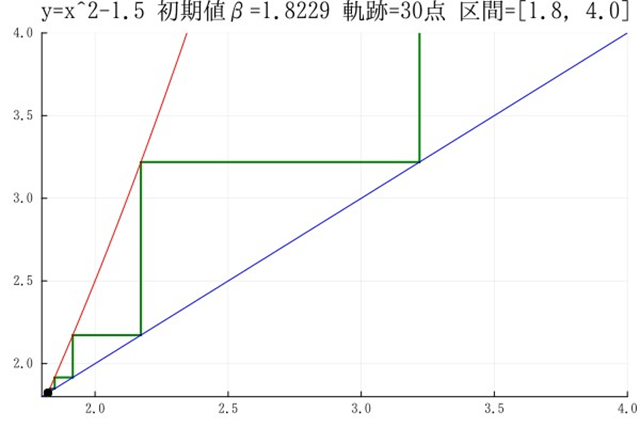
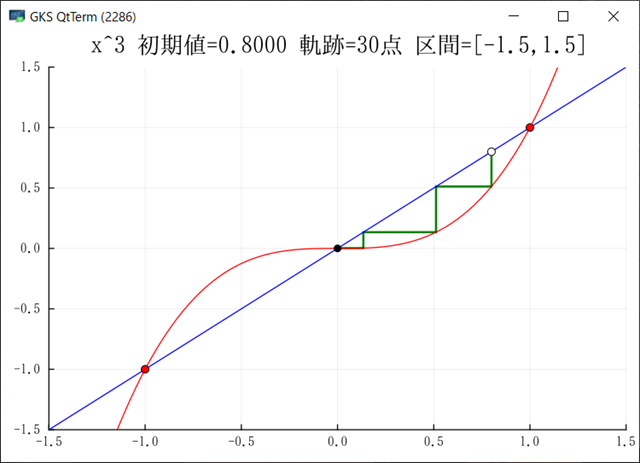
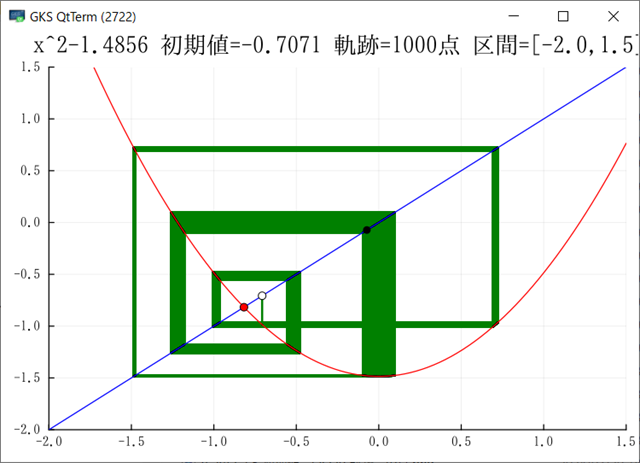
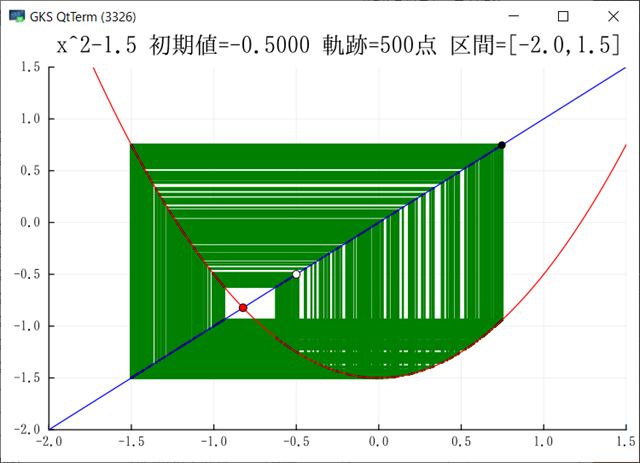
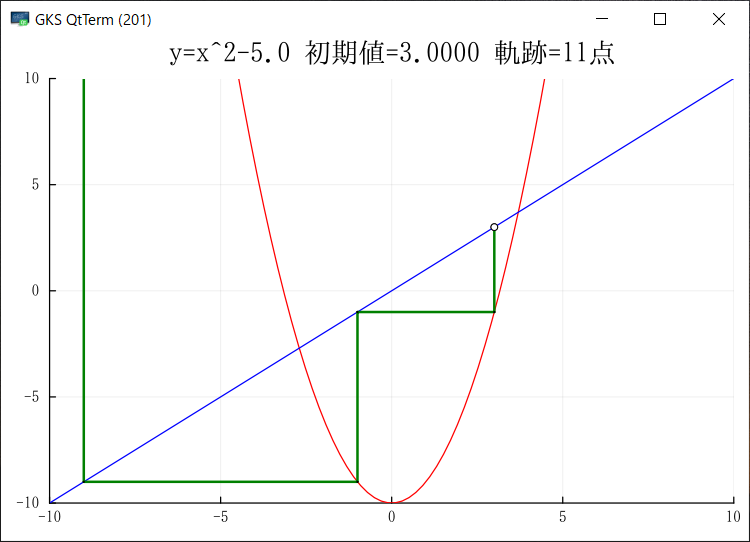
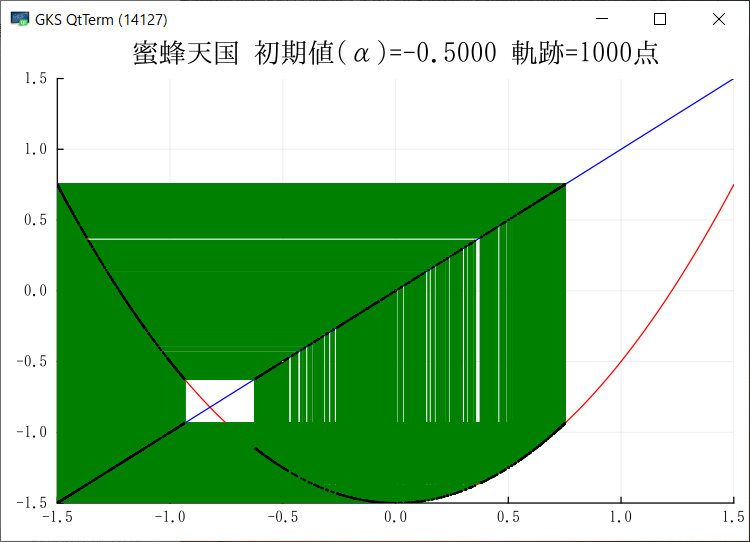
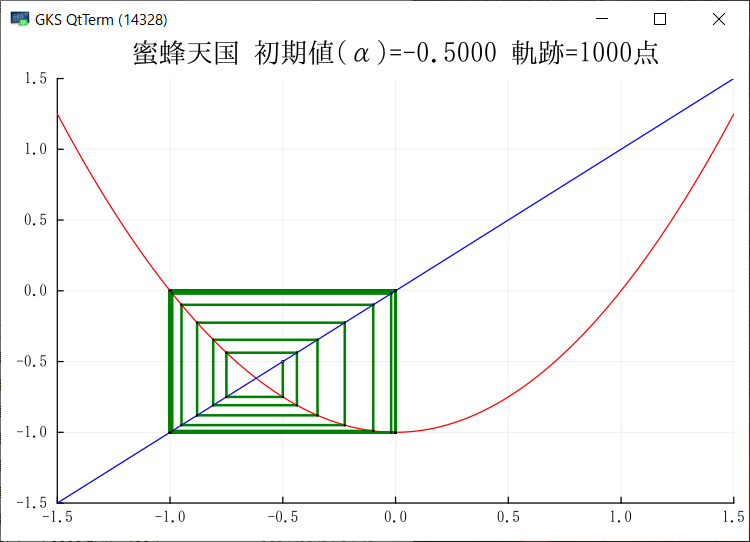
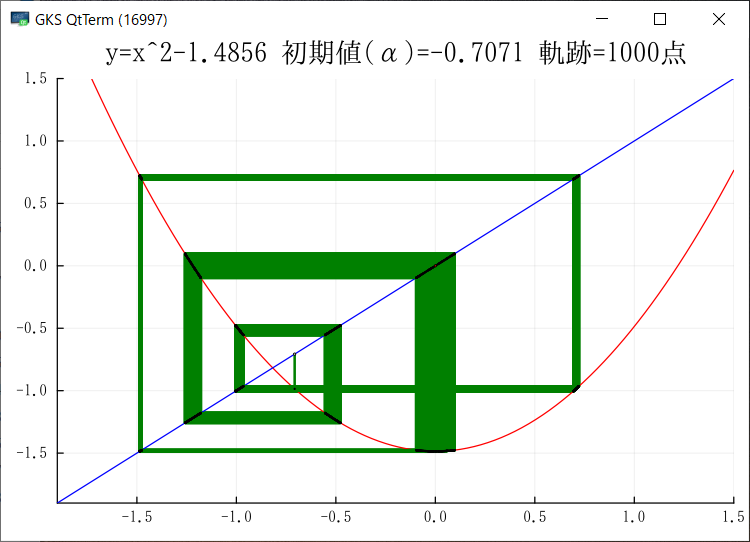
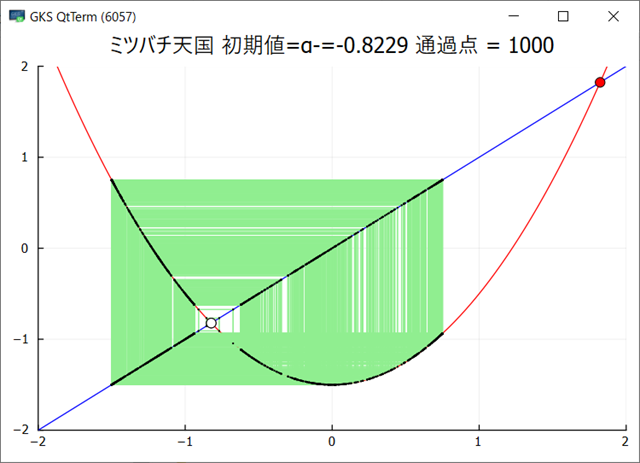
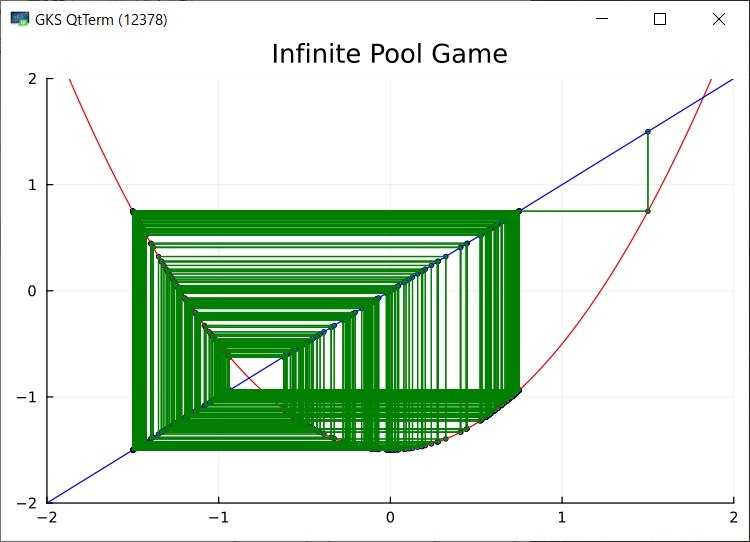
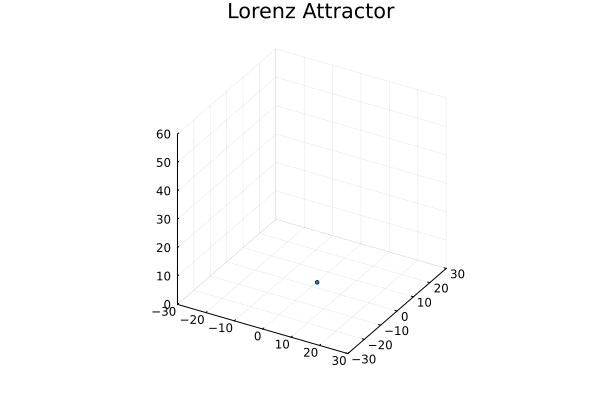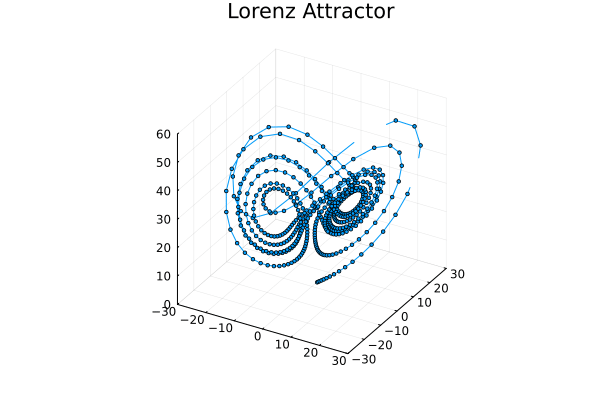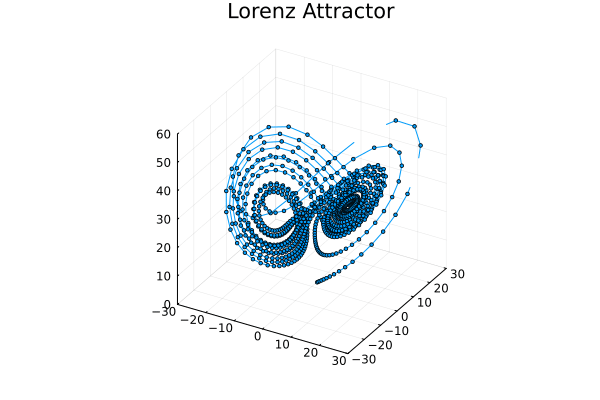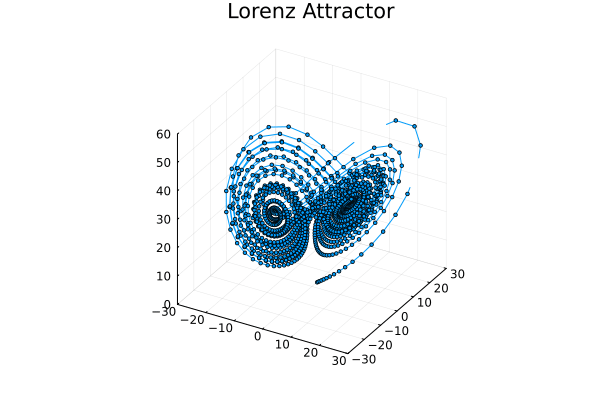
Julia でグラフを出力できるようになった.複数のサンプルが動くようになったので,もうほとんど大丈夫だろう.グラフをGIF出力ではなく画面にも出したいのだがどうしたらよいのだろう?module_Foo.jl には画面を出してキー待ちになるサンプが入っている.このサンプルでは先にプロット配列を生成し,それをまとめてプロットしているのだが,ループの中で毎回プロットするようにできるだろうか?
Plots の辺りをもう少し勉強しておいた方がよいのではないか?とりあえず,Home – Plots を通読してみよう.
https://docs.juliaplots.org/stable/
Processing Pipeline という項目に出てきたサンプルを実行するには,PythonPlot パッケージが必要だ.解説では,backendは自由に切り替えることができるという話なので,インストールしても問題は発生しないはず.やっておこう.⇒かなり時間が掛かる.ギガを使い切っているので,最後まで終わればラッキーというところだ.19/20のところで手間取っている.1Mbpsくらいは出ているのだが… Ponta ポイントが4165あるので使ってみよう.インストールは完了したが,VS Codeでは別途インストールが必要だ.
Julia REPL では一応動くが,グラフは表示されない.VS Code ではエラー(警告)になる.いずれにしてもグラフは出ない.
Warning: backend `PythonPlot` is not installed.
└ @ Plots C:\Users\babalabo\.julia\packages\Plots\a3u1v\src\backends.jl:43
┌ Warning: Keyword argument `orientation` is deprecated.
│ Please use `permute` instead.
└ @ Plots C:\Users\babalabo\.julia\packages\Plots\a3u1v\src\args.jl:1552
同一内容の別サンプルではSVGを出力している.こちらは動作している.
MyVecWrapperというのも出してみたが,やなり画面は出ない.ただし,これを動かすには using Plots を追加する必要がある.おそらく基本的なコードは既知であるという前提で省略されているのだろう. terminal に出力する UnicodePlots というのをインストールしてみた.あまり関係なさそうだ.
The graphic is not shown implicitly, only when “displayed”.
とあるので,ともかく Display しなくてはならないのだろう.gui()で表示できるようだが,やはり,ポーズを入れないと見えない.
A Plot is only displayed when returned (a semicolon will suppress the return), or if explicitly displayed with display(plt), gui(), or by adding show = true to your plot command.
ということなので,show = trueでもよいのかもしれない.しかし,いずれにしてもプロットの最終結果を表示ないし保存というのが基本的な考え方のようだ.Makie というのがある.使えるかもしれない.JuliaのEXEをビルドするコンパイラというのがある.PackageCompiler という名前だ.GTKというのもある.
https://goropikari.hatenablog.com/entry/julia_gui_app
Julia REPLでは冒頭でgr()を実行することでウィンドウが開いた.いや,REPLでは何もしなくてもウィンドウが開く.つまり,うまくゆかないのはVS Codeの場合だけだ.⇒JL HUB というサイトを見つけた.公式マニュアルより,こちらの方が分かり易いような気がするので,先にこちらを読んでみよう.mmm… 自サイトの中でリンク切れになっている.大丈夫かな?⇒これは,解説書というより,関数リストのような作りになっている.読み物にはなりそうもない.これはどうだろう?
Displaying computation results in Julia
https://subscription.packtpub.com/book/programming/9781788998369/1/ch01lvl1sec20/displaying-computation-results-in-julia
この記事ではPyPlotが必須なのでインストールした.⇒MyPlot というのはかなり大きなパッケージのようだ.using MyPlot で相当な本数のモジュールが展開されている.
using PyPlot, Random
function f()
Random.seed!(1)
r = rand(50)
@show sum(r)
display(transpose(r))
print(transpose(r))
plot(r)
end
f()
このコードでは,@show, display, print, plot の4つの手続きが呼ばれている.実行結果は:
done
sum(r) = 24.687009959109595
1×50 transpose(::Vector{Float64}) with eltype Float64:
0.0491718 0.119079 0.393271 0.0240943 0.691857 0.767518 0.087253 0.855718 0.840384 0.89077 0.138227 0.347737 0.198521 0.00819786 0.592041 0.801055 0.564185 0.327726 0.977264 0.0994036 0.972564 0.124189 0.941894 0.983662 0.743445 0.805318 0.989476 0.839891 0.117166 0.291122 0.114068 0.43047 0.570276 0.53366 0.825586 0.32119 0.279424
0.682005 0.805025 0.211005 0.267188 0.343875 0.440831 0.116041 0.547515 0.589217 0.19932 0.364128 0.802561 0.661425
[0.0491718221481211 0.11907881640750706 0.3932710232252806 0.024094310524527707 0.6918572875342215 0.7675180540873912 0.08725304891274233 0.8557176841095734 0.8403841370820818 0.8907696748195567 0.138227024723224 0.3477368477058109 0.19852090963358837 0.008197858843363659 0.5920407556271403 0.8010551449181886 0.5641848519912193 0.3277260730851096 0.9772642076169137 0.09940363694051435 0.9725641606703476 0.1241890127157469 0.9418941527940101 0.9836615941923371 0.7434447269076069 0.8053175847115641 0.9894764460236303 0.8398907896025322 0.11716604842787648 0.29112215301979427 0.11406795780290624 0.43047012103110294
0.5702762508836267 0.5336600074808578 0.8255859228330473 0.3211901705171226 0.2794235399691639 0.6820050160336559 0.8050245353412276 0.21100502806555133 0.2671882107649258 0.3438753675415538 0.4408314844038338 0.11604055879014974 0.5475146896778691 0.5892167646241558 0.1993200843257663 0.3641283484132992 0.8025607099234905 0.661425351684768]
のような感じだ.rというのは乱数配列でサイズは50,@show sum(r) ではこの配列の和を取って,それを表示している.この配列は1×50でこれを転置して 50×1のベクトルとしたものをdisplya, print しているが,この2つの違いは小数点以下の桁数の違いだけだ.display では 0.0491718,print では 0.0491718221481211 となる.JuliaのREPLではplot()の結果は見えてこない.VS Code の julia terminal で以下を実行する. julia> include(“display.jl”)
showとdisplayまでは動作するが,plotでエラーが発生する.
Please submit a bug report with steps to reproduce this fault, and any error messages that follow (in their entirety). Thanks.
Exception: UNKNOWN at 0x7fff2fc7cf19 — RaiseException at C:\WINDOWS\System32\KERNELBASE.dll (unknown line)
in expression starting at none:0
RaiseException at C:\WINDOWS\System32\KERNELBASE.dll (unknown line)
画面はちらっと見えるがすぐ消えてしまう.出口で realdline を実行しても同じだ.include(“display.jl”)をJulia のREPLで実行すると動作はしているようだが,画面をちら見せして消えてしまう.readlineは効いていない.下のようなグラフが表示されるはずなのだが…
plotの後に,show()を追加すると,VS Codeでも画面が出るようになる.ただし,エラーが起きてすぐに閉じてしまう.plotの引数にshow=trueを追加しても効果なし.⇒PyPlotをPlotsに変えて動作するようになった.今度はplotの引数でshow=trueが効いた.出口のreadlineは必須だ.どうも,このやり方しかないような気がする.これかな?
https://docs.juliaplots.org/latest/output/