Collatz formulas are like a black Hole of natural numbers – さあ，もう一度ゼロから始めよう

The Beginning

I’ve been running a long long project for more than 25 years that’s still unfinished and the target program Zelkova Tree genealogy builder wasn’t ever formally released. One day I received a mail from a core supporter of the program. Apparently it seemed that he was almost mad at me and said “I’m checking your mail account still alive or not”. It’s a matter of fact that I hadn’t worked at all since April of this year, that is about a half of one full year. I thought I had to work now anyway and stood up to get started.

But I had had something left behind and decided to spend a small amount of time for the subject, that is, the Collatz conjecture. I worked on it for about one or two months and once abandoned. But as you know there remained a strong desire to meet again just once more. It was definitely destined to be my last chance for challenging the problem and I was fortunate enough to encounter this page on the net. If not I would failed again as expected although I myself conceived some other strategy in mind.

This is a wrapping up of the record of the discussion at a Facebook group for natural science. NM (Noureddine Mohiti) is a young amateur mathematician in Morocco and MN (Michiro Nasu a.k.a. Baba Age) is me, an aged programmer in Japan.

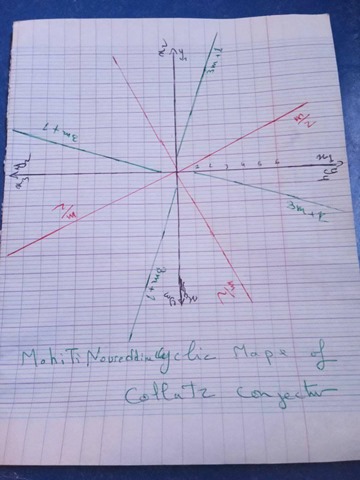
NM: Collatz formulas are like a black Hole of natural numbers

MN: Intriguing! How about this.。

NM: Yes. But how can I represent Collatz graph in your graph

MN: Noureddine Mohiti, I think my graph is essentially equivalent with yours if I understand you correctly.

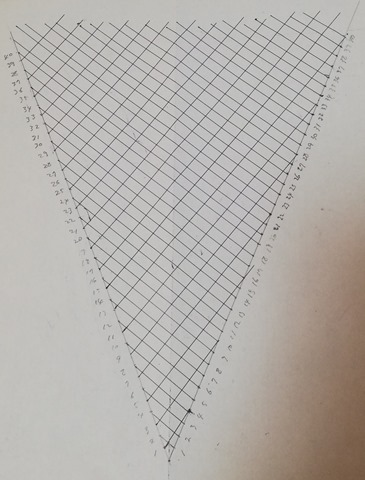
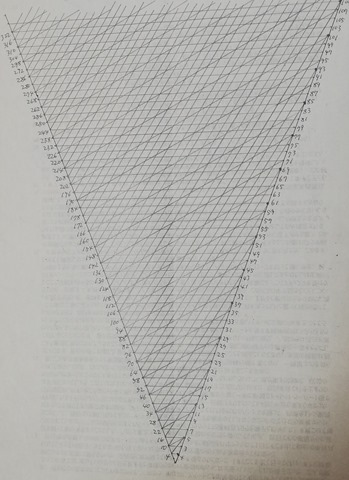
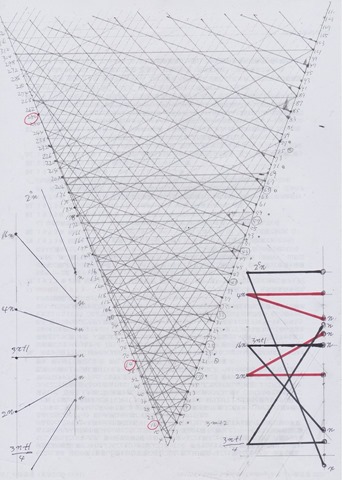
My graph is set on 2-D Euclidean space (not Cartesian space) and it’s horizontal/vertical lines (axes) are 2 natural number [half straight] lines which begin at the origin and go to the opposite direction respectively.

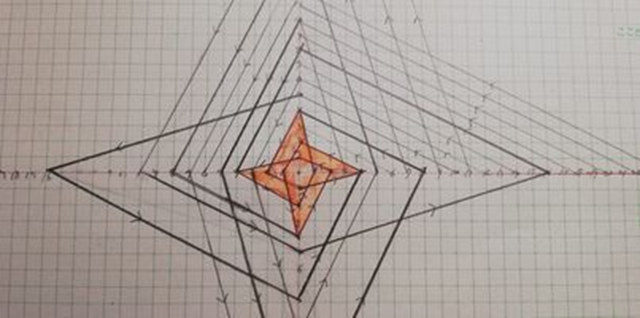
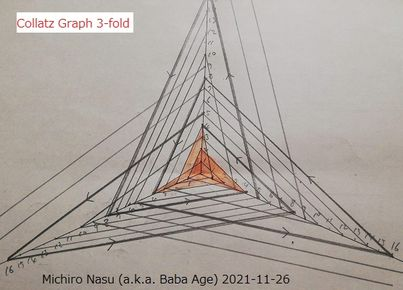
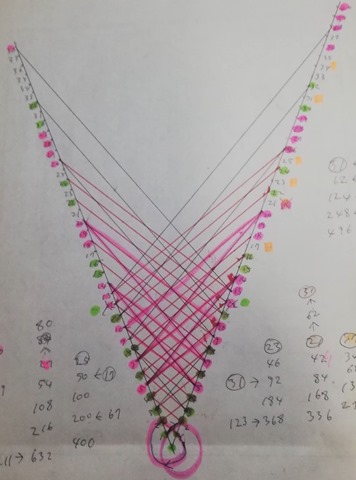
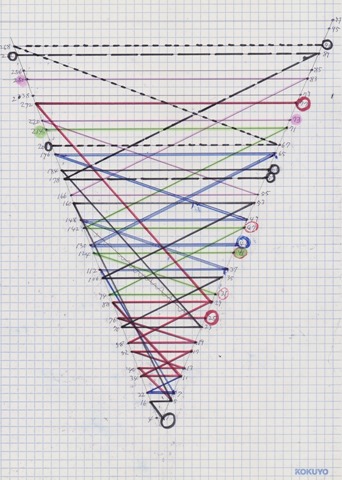
Remarkable point of this drawing is that it is rotational symmetry in 4 fold. I’ll show you another pattern of 3-fold.

Collatz Graph 3-fold

Colored shape at the center is your Black Hole! Never look at the hole too closely otherwise you would be dragged into the hole upside down. Arrows are Collatz operation like 3n+1 or n/2.

After drawing this graph, all we need to solve the Conjecture is just to show that the graph is connected. Can you?

NM: When we reversed the formula of Collatz we must provide two parts
#The part one is _any Odd number can be expressed as (2^a × y – 1)/3
y is an odd number and a is a natural number
_ any even number can be expressed as 2^c × y
y is an odd number and c is a natural number
_ part two for any N numbers expressed as above must N+1 can expressed as above
Then Collatz conjecture correct 100%

MN: Noureddine Mohiti, Sorry, later…

NM: Age BabaAge BabaAge Baba about what

MN: Noureddine Mohiti, Your theory doesn’t work for a variation of Collatz sequence. Apply 3n-1 formula instead of 3n+1 in Collatz and you will see.

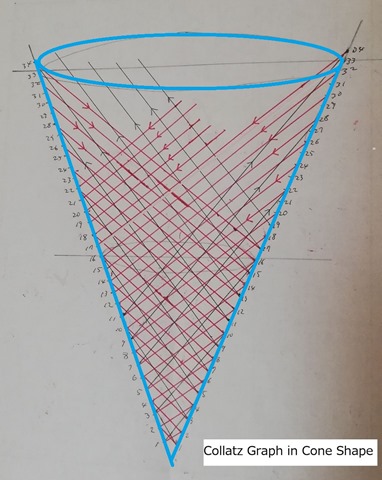
NM: Can you draw this graph in 3D

MN: No, I can’t. But why?

Now I understand what you meant by 3D. I’m going to try it.

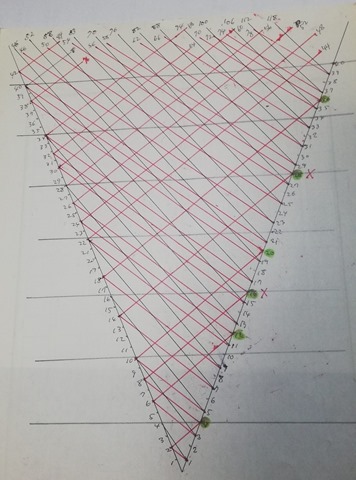
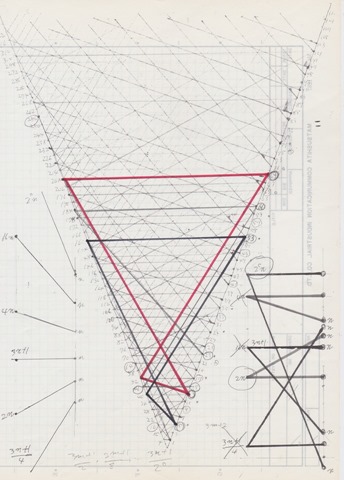
The 3D Cone shaped 2-fold Collatz graph

Here it is! 3D drawing cone shaped 2-fold Collatz graph.

In your mathematical induction “for any N number expressed as above” is equivalent to cut the cone horizontally at N position. But the cross section is problematic because a lot of arrows are going out through the cut surface. Apparently if N+1 is even then it may be OK otherwise you are lost.

I want to try to separate odd numbers and even numbers.

[Too early] CONCLUSION:

Your intuitive notion “Collatz formulas are like a black Hole of natural numbers” is admittedly precise. We are watching a ball ceaselessly rebounding in a cone shaped basket and expect that the ball will eventually drop down into the pocket at the bottom of the basket. Collatz conjecture is based on the assumption that the gravitation is universal. As far as we glimpse Collatz graph 2-fold, it looks like simply true and natural. Right?

But beforehand what’s the “gravity” in this case. The ball goes up when its value is odd and goes down in the case of even. Those are said to be repulsive/attractive force. The question is why you are so confident that the attractive force is much stronger than repulsive one. Indeed attractive force works only in order 1/2 (one half) while repulsive force does in order x3 (triple).

Nevertheless empirical fact appears that every balls (without exception) are eventually caught by the trap so far. Supposedly this is because the frequency of occurrence of even numbers is greater than odd numbers. An odd number turns even at once but an even number is possible to stay even for a while (or to the last in case of power of 2). However number theory must be a mathematics(strict science) but not a part of probability theory. So we shall not assume that the gravitation is always universal.

What happens if the gravitation collapses? Maybe the ball will go on and on and keep floating and circulating in the sky like a satellite or otherwise boost to the outer space escaping from the gravity zone like a space ship heading to alternate time-space. Nobody knows so far.

PS: if you can show that the Collatz graph is connected then you are the winner. M.N. 2021/11/26 [With this “CONCLUSION” I was almost going to leave the discussion at the time, but …]

NM:

MN: What’s the point?

NM: What can I show ?

MN: You have to prove that the Collatz graph, which is an infinite graph, is connected as a whole.

NM: Yes I understand

MN: I believe that we’ve almost done. At this stage to continue this discussion we (馬場英治 and Noureddine Mohiti) have to make a solid contract with respect to confidentiality (kinda nondisclosure agreement). Would you promise me you’ll NEVER EVER BLOCK me as a Facebook friend. Because if you do so I’ll lose all of my important comments here (and credentials thereof) as you are the contributor of this thread. Do you agree with me?

NM: Age Baba, I promise you I never ever block you

MN: Thanks a lot, my eternal friend!

Have fun with Magic Floating Ball!

The ball is keep floating while buoyancy working

NM: Age Baba, can you help me to create an algorithm program deal with Collatz formula

MN: We need neither a program nor an algorithm. Just prove it. It’s simply impossible to analyze an infinite graph with any algorithm in finite time…

NM: Age Baba, the program is to deal with a trick in binary formula of numbers

MN: That’s interesting but I have no idea around there for now.

It is easy to check if a number is even or odd. Just check the LSB of binary number. Also to apply Collatz operation is easy. Just right shift for n/2 and left shift and plus n+1 for 3n+1. But how can you check the MSB of an infinite number? Power of 2 is a number like MSB=1 and the other bits are all 0.

What language do you use to write a program?

NM: The key ️ take is that :in binary formula any numbers can expressed combination of natural numbers {a,b,c,…0} ; a>b>c>…¢>1>0 the Party is how the numbers ¢ change under Collatz conjecture

MN: I’m not sure what you meant…

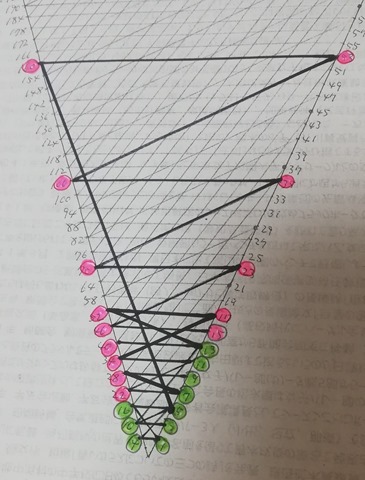
Collatz 3n-1 version graph as a deadly Counterexample

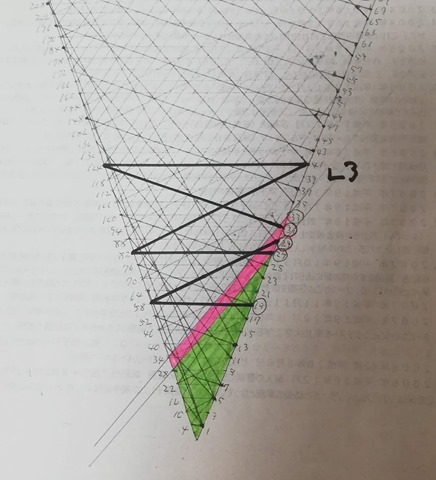
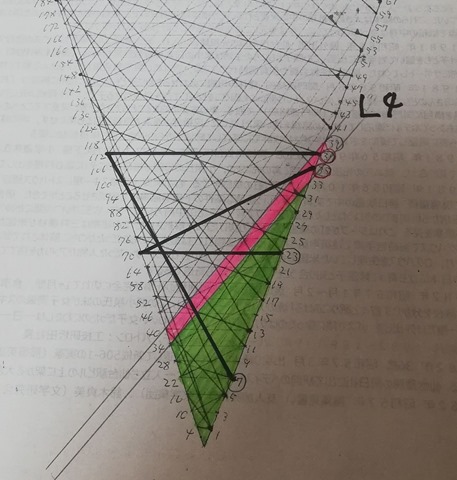
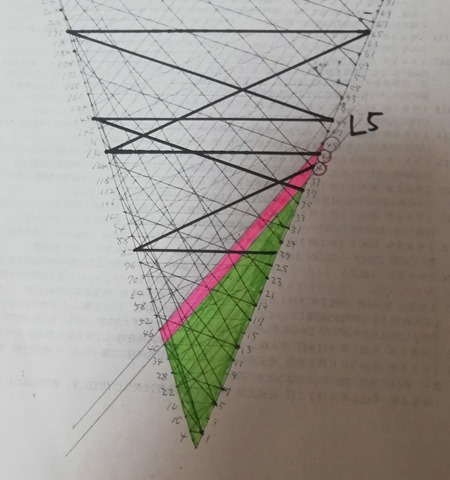
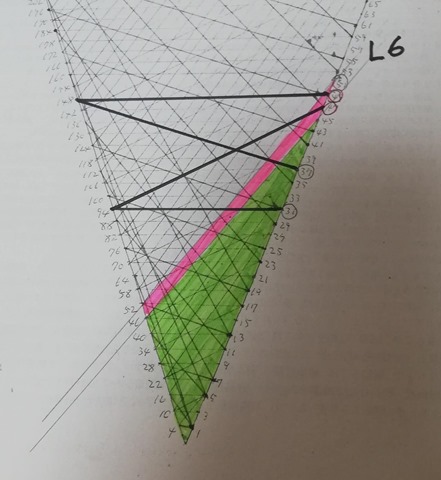
Firstly I want to show you Collatz 3n-1 version.

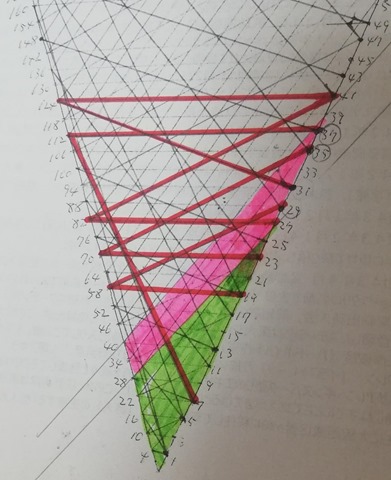
Obviously Collatz 3n-1 version graph is not connected. In this picture, pink points and green points belong to different components respectively. Can you see?

I hope now you understand what was wrong or where you failed at with your theory.

I’m sorry for such obscure dot color in the top corner of the cone. 1, 2, 3, 4, 6 and 8 dots are green and 5, 7, 9 and 10 are pink. Obviously 0 dot is of no use (just a place holder).

There are at least two cycles in the Collatz 3n-1 version graph. One is {1, 2} cycle in green color and the other is {5, 14, 7, 20, 10} cycle in pink.

Thus Collatz conjecture does not hold on Collatz 3n-1 version.

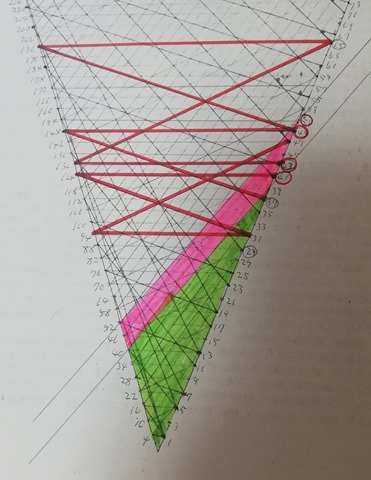
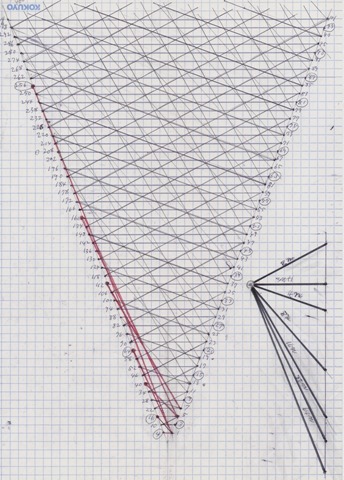
That’s it. Now let’s return to the formal version of Collatz graph. This is one surface version of cone-shaped Collatz rotational symmetry in 2-fold graph reducing a number of lines to make it easily readable.

This is pretty tricky job to do and I mistook 2 places. I don’t know those defects are repairable or not so far.

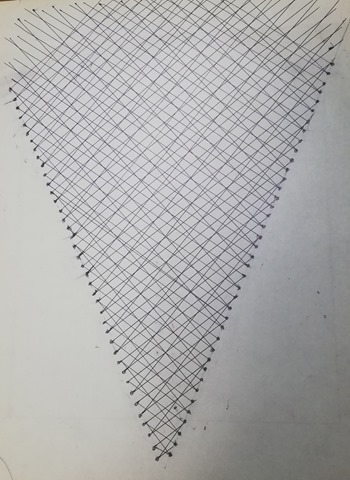
But at first I’m going to upload the most dense version of the graph to make you convinced that the graph is really connected.

NM: like a Black Hole made of mirrors

The Collatz basket cone shaped

MN: This is the Collatz Basket Cone Shaped.

I’ve mistakenly drawn one extra line, but it doesn’t matter.

The most significant point is that we need not a color pen any more. Can you guess why?

How can you imagine this basket is decomposable. If you think so I’ll dare to say you are insane.

Now I want to finish one surface model. In this model two things are required. (1) the number of lines must be reduced to a half, (2) still it must reserve the characteristic of rotate symmetry. This task is not so hard as the full version figure seems to be line symmetry. So allocating two lines pair at the line symmetric position to each surface may be enough.

I mentioned earlier that the most significant point is that we need not a color pen any more. Pen color signifies the attribute of a line. There are two types of lines. one is red which designates n/2 operation and the other black one designates 3n+1. That is, red means descending lines and black ascending lines. Original graph is a directed graph but as far as we consider connectivity, line direction is of no interest. Why?

I reserve the answer for your task. Prove or disprove this:

As far as Collatz graph is connected (as an undirected graph) it does neither circulate nor diverge other than cycle(1, 4, 2).

NM: Yes you can Draw a trajectory of any natural numbers drop in small cycle (1, 2, 4) like black holes

Algebraically the key is in the binary formula of natural numbers

MN: Noureddine Mohiti, But you couldn’t prove it.

NM: Age Baba, the first proof continue two parts I say that is my proof. But the binary formula I work in it

MN: Give me the link to your page.

That’s an observation, not a proof.

NM: I write a line I think it is a proof

MN: Noureddine Mohiti, Where?

What’s required to prove the proposed proposition is just an elementary level knowledge of graph theory. Didn’t you learn graph theory?

As far as Collatz graph is connected it does neither circulate nor diverge other than cycle(1, 4, 2)

OK. I’ll show you the answer.

Proposition: As far as Collatz graph is connected (as an undirected graph) it does neither circulate nor diverge other than cycle(1, 4, 2).

Proof: Let G(V, E) be the Collatz graph such as V is a set of natural numbers (except 0) and E is a set of directed edges e(i, j) where if i is even then j=i/2 otherwise j=3i+1. Apparently every vertex v(i) in G has only one outgoing edge e(i, j).

Assume that G is connected and it has two cycles C1 and C2. Since G is connected there must be at least one undirected path p(V1, V2,…, Vx,…, Vj, Vk) between C1 and C2 while V1 is a vertex on C1 and Vk is a vertex on C2. Obviously the orientation of e(V1, V2) and e(Vk, Vj) are opposite. Hence there must be a vertex Vx which has two outgoing edges. This contradicts to the premise.

Similarly the infinite divergence case is also rejectable. Therefore since graph G already has a cycle (1, 4, 2) it does neither have any more cycles nor diverge into an infinite space. Thus Collatz Conjecture is true as far as Collatz graph is connected. QED

I finished 2-fold Collatz graph one (half) surface version.

This figure is too simple to fail drawing

I want to ask you how many lines do you need to draw this graph or how many wires do you use to knit this basket. Consider you actually are going to make this basket in real. How many wires would you purchase at the DIY shop near by?

If this graph is an Euler graph then just a single wire is enough for you. Because Euler graph is drawable by just one pen stroke. Euler theorem says “A connected graph has an Euler cycle if and only if every vertex has even degree”.

However in this graph innumerable T letter intersections appear. That is, it has a lot of odd degree vertices. To see this more clearly I’m going to erase left and right side lines in this picture.

Look at this.

You might think that those lines are totally disjointed. But it’s not true.

This is a 3D model object of cone shaped Collatz graph. So you have to imagine that there exists another surface at the back of the front surface.

Or otherwise you can connect two points at the same horizontal position by drawing an additional horizontal line between them as these vertices are actually/theoretically the same.

And then you will notice that the joint point (end point) of a line rising to the right side line really makes a T letter intersection.

Could you count the number of wires necessary to knit this neat basket? Of course you cannot make a complete wire model that represents the Collatz graph perfectly even if you purchase all of metal wires on the earth as it is an infinite graph.

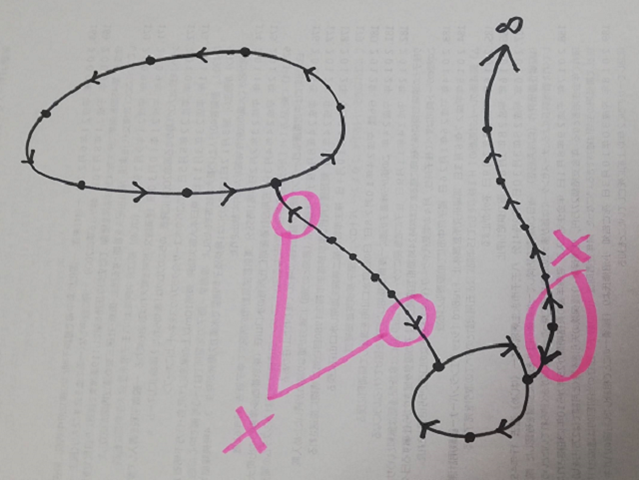
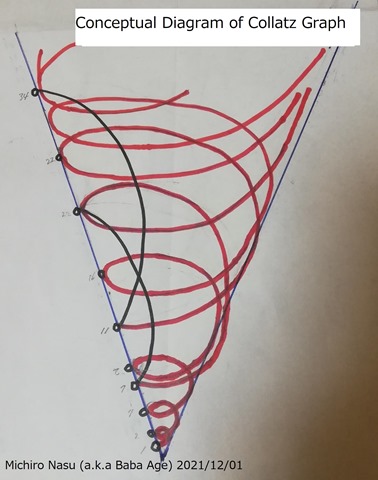
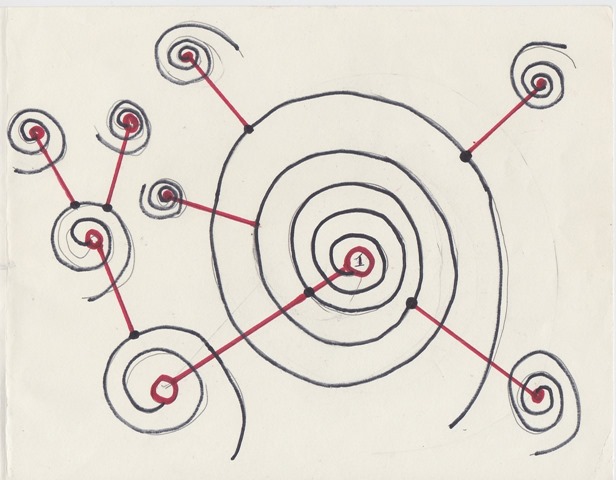
Mohiti Spiral Diagram of Collatz black hole

Here comes conceptual diagram of Collatz Graph to see how it looks like.

I want to call this as “Mohiti Spiral Diagram of Collatz black hole”.

NM: Age Baba, Great that is the most beautiful graph

This day I am ill .

I will work in point to explain that not exist any cycle in Collatz conjecture

MN: Sorry for that. Take care!

Mohiti Spiral Game a smartphone app

MN: Can you write a smartphone app named “Mohiti Spiral Game” for advertising your Collatz black hole theory? In this game a ball is rolling down and up through the spirals until it is caught into the black hole. Users input a natural number and press GO button. That’s simple.

NM: We can write it as Age-Mohiti

MN: Noureddine Mohiti, Great! Let’s go.

NM: Age Baba, Ok
But I don’t know how to create this game
But I don’t know how to create this game in smart phone

MN: Ouch! You have to learn how to write a code for smartphone. A lot of information are around on the net.

I suppose you are young and to learn a programing language for smartphone device will not be your time loss.

NM: Age Baba, HHh I can see some videos in YouTube and create it I will see

MN: Don’t hurry. Slow and steady wins the race.

I believe you already have the number of wires to knit the Collatz basket. How many wires do you guess?

NM: I really don’t know I treat Collatz by three methodologies (the inverse formula . The binary system. The graph as black holes) and some ideas from meta-mathematics they are very strange but make me feel of Life , feel of heart ❤️ beating

MN: Noureddine Mohiti, (1) The inverse formula: This is the most painful way to go onward. It had been causing every trouble and difficulty in this domain. (2) The binary system: Binary format is useful for practical purpose for the reason of efficiency but of no use for theoretical proof. (3) The graph as black holes: This is your original idea although every researcher has felt like that but never faced up squarely. I greatly appreciate you for this point.

One more point I owe you is your request to make 3D diagram. It led me to the rotational symmetry in 2-fold graph and I could come up with the brilliant invention of Collatz Cone Basket which was itself the long sought door. It is truly an inverse approach none of researchers could find out.

NM: Never forget million problems they make you learn more is not about money is about to feel happy

MN: If it happens to me in the near future to write an article for this subject you must be the honorable coauthor of the article. Ok?

Knit a Collatz basket with curling wires from scratch

Are you ready? Now it’s time to make Collatz basket from scratch. We have provided wires for this purpose.

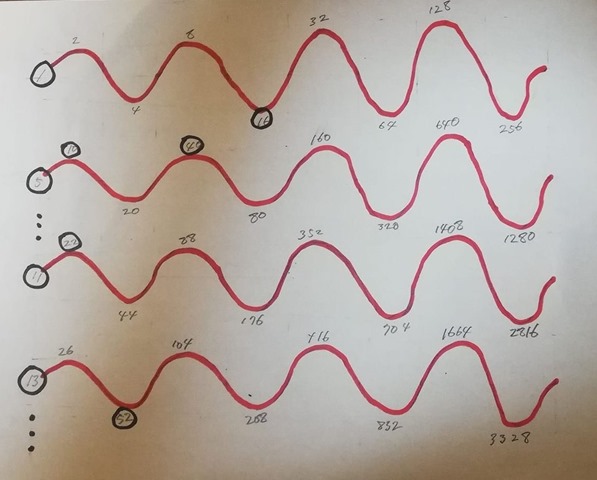
These wires are so to say lists of numbers. Top of a list is an odd number n followed by numbers like n, 2n, 4n, … 2^c * n. Accordingly the number of wires is N/2+1 provided that N is the biggest number in the basket.

Let’s start.

This is the main tree but if you cannot find the place for some wire n in this tree you are free to allocate it to the other wire which has the number (3n+1). As you see, this is a tree and adding a subtree at an arbitrary node doesn’t change the topology of the graph. For sure!

This is the Collatz graph! It is definitely a tree and therefore connected. To give orientation to each edge doesn’t change the connectivity of the graph. To make formal Collatz graph you need to add an extra edge e(1, 4) to the graph because 1 is another odd number which we missed in the first truck.

This makes a small directed cycle on the graph but never makes other cycles because you need not add any other edges to the graph. Obviously every node on this graph eventually goes down to the root of the tree. Thus Collatz conjecture was proven. Today Collatz conjecture turns to be a theorem.

I’ll give you a bonus diagram !

The previous graph is too redundant and can be reduced like this by removing red curling lines in it. Red curling line is equivalent to a spiral line which ends at an odd number in Mohiti Spiral Diagram. Therefore all of numbers In the right hand tree are odd. You see?

One more bonus from Wiki. This is a deployment of the tree above of which vertices are totally odd.

Directed graph showing the orbits of the odd numbers less than 50 (with the exceptions of 27, 31, 41 and 47, because they would make it too tall) under the Collatz map.

Every researcher had stumbled at this tree. Trying to get the complete orbits of the odd numbers is the worst scenario conceivable.

I want to revoke my previous argument. As always Collatz 3n-1 version was found to be its counterexample.

But it’s too early to give up. We still have a back hand.

The final fight revenge after 20 years

I’ve kept an bottle of vintage wine aging for 2 decades carefully put aside. It is an unfinished article written by myself and abandoned for a long time. Fortunately we can still access it on the net at SEMANTIC SCHOLAR.

Strongly Intransitive Graphs and The Perfect Graph Conjecture

It was written in 2001 for arguing the relevance of graph transitivity to the strong perfect graph conjecture. Semantic Scholar mistakenly put the name of Hungarian mathematician Tibor Gallai (1912–1992) as the coauthor of the article but it is untrue. Gallai already passed away before 2001. Of course it’s my extraordinary honor to find my name next to the eminent mathematician’s.

The strong perfect graph conjecture as well known as Berge’s conjecture was finally proven in 2006 by Chudnovsky, Robertson, Seymour and Thomas. By the way what’s the perfect graph about?

In graph theory a perfect graph is a graph in which the chromatic number of every induced subgraph equals to the order of the largest clique of that subgraph (clique number). A hole is a chord-less cycle on five or more vertices and n-hole designates a hole with n vertices. An odd hole is such an n-hole as n is odd. The complement of an odd hole is called an odd antihole.

A graph with no odd holes and no odd antiholes is called a Berge graph. A Berge graph is obviously a perfect graph and Berge’s conjecture states that every perfect graph is a Berge graph. This implies that a graph is perfect if and only if its complement is perfect [Perfect graph theorem]

The counterexample above has a 5-hole !!!! Got it?

NM: ❤️❤️❤️❤️

MN: This is my final fight revenge after 20 years. ⚡️

NM: Revenge of what ?

MN: Involved in the battle over Berge’s conjecture.

The Collatz bipartite graph and the odd Collatz tree

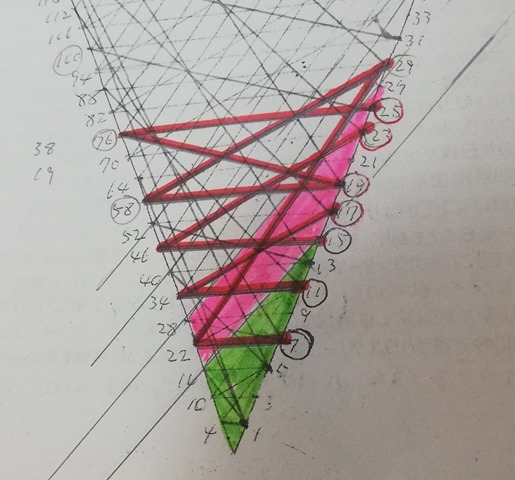
Look! As I said earlier I successfully separated odd numbers and even numbers.

Odd numbers are on the right side line and even numbers are on the left. A horizontal line connects odd number n and even number 3n+1. The gap between two even numbers equals to 6. All other even numbers are omitted in this graph. The remarkable point of this graph is its total regularity.

The right side odd numbers are 1-to-1 correspond to the left side even numbers. In this basket we could put even numbers up to 322 and odd numbers up to 107. Maybe we can analyze a bit larger area than before. I believe this will be an enough formulation for the final proof.

Our goal is to prove that this graph is connected (as an undirected graph). How can we do that? The most significant point is that we don’t care the orientation of the edges, i.e. the orbits or trajectory of the nodes.

Let’s go onward! First of all I want to repost the contracted Collatz tree. This tree is made from the Mohiti Collatz Spiral diagram reducing all of the redundant spiral lines in it. As you see easily this is almost equivalent to the bipartite (even/odd separation) Collatz graph shown above.

[The above contracted tree is almost equivalent to the Collatz bipartite graph but not exactly the same. In the Collatz bipartite graph none of even number is adjacent to an even node but in this graph even nodes form a chain following the top odd node.]

By the way “Go Onward” was the habit of Vladmir Z. Nuri who presided over a mailing list named theory-edge for pursuing cutting-edge science especially unsolved open problem in the beginning of the millennium.

To compare these two graphs I allocated all the numbers in the contracted tree to the bipartite graph.

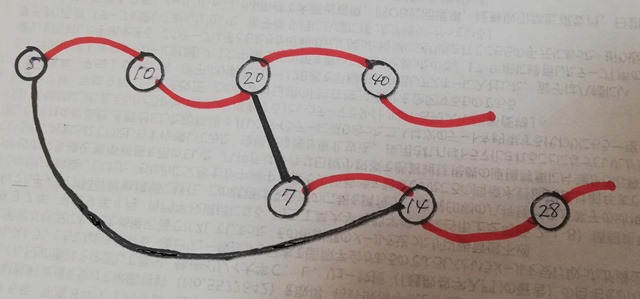
As you see every vertices in the contract tree are in the bipartite graph. These vertices are obviously connected except 1. As this graph was intended to be bipartite we don’t have edges among even vertices. Instead to connect 16 and 4 I added an edge between 16 and 1. With this adjustment every vertex come to join with adjacent vertices and the induced subgraph turns to be connected.

I’m sorry, the graph above was still disconnected. We have to add one more edge(52, 13).

Good!

Now we can safely assume that every numbers under 16 in the bipartite graph are connected. Of course this assumption involves a portion of numbers over 16 but the formulation is undoubtfully acceptable.

But before we proceed we had better check how many numbers are involved for establishing the connectivity of the numbers under 16 in the bipartite graph.

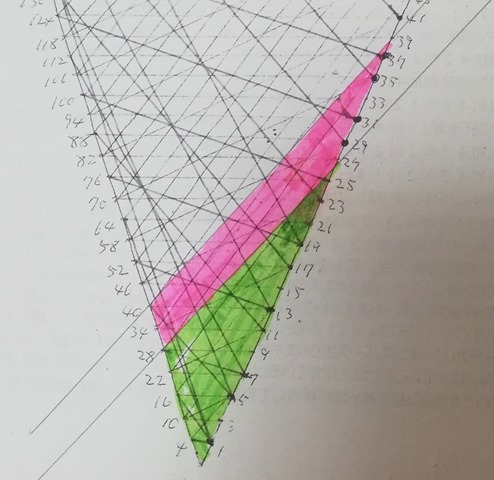
I added one extra edge(160, 5) to establish the connection between 15 and 5. The number of outside vertices involved in this connection is 14.

Numbers under 16 are colored green and outside vertices involved are pink.

Slicing the bipartite Collatz graph into layers for mathematical induction

Our strategy for the mathematical induction is slicing the bipartite graph into layers in some way or other.

Our consideration is whether it is possible or not to show that if every vertices in layer N and the all layers below N are connected then every vertices in layer N+1 are connected by using the regularity of the graph.

Here is a good news. We know that every number with value 3m i.e. a multiple of 3 is a leaf in any Collatz trees. In other words there is no trajectory from any other numbers to a number of multiple of 3 in the graph. This means we can neglect the connectivity of one third of odd numbers. That’s a great advantage and would relax our difficulties to a considerable extent.

Every even number in the bipartite graph joins to an odd number by horizontal line in the bipartite graph. Therefore all we need to do is only to show the mutual connection between odd numbers.

This is your task: Prove the proposition below.

Proposition: Let number n be a multiple of 3. Then there is no trajectory (a sequence of Collatz mapping) from any other numbers to the number n. (This implies that there is no multiple of 3 in the even numbers allocated on the left side line in the bipartite graph).

Let us see how it looks like. At first we begin at layer 1 which has 3 even numbers {4, 10, 16} and 8 odd numbers {1, 3, 5, 7, 9, 11, 13, 15}. Assume that these vertices are connected. Layer 2 has 2 even numbers {22, 28} and 6 odd numbers {17, 19, 21, 23, 25, 27}. All we need to do is to show that all these odd numbers are connected to layer 1 vertices. However as I said above 21 and 27 are to be neglected because they are multiples of 3. Therefore our necessity is to show only 4 odd numbers {17, 19, 23, 25} are connected with layer 1.

NM: I told you that you must look for the relationship between the graphs of the numbers (a, b, a×b).

But will find a problem with prime numbers

MN: I’m not sure what you mean. Would you please elaborate a bit more.

NM: You make three graphs of three numbers (a, b, a×b)

MN: No, I don’t.

NM: Why prime numbers because you can’t factor prime numbers

MN: And then what?

NM: I don’t know is beautiful experience

MN: I have no idea what’s your experience about.

Noureddine Mohiti, Now I understand what you are trying to say. You are still stick with your first picture on this thread. What a surprise! But I’ll show you how you can draw the picture.

Your insight is good but your approach is not optimal. You selected Cartesian space to draw because your aim is to solve the problem by algebraic geometry way. It might be quite a natural thought.

I recommend you separating odd numbers and even numbers on the axes. Suppose that odd numbers are lined on the x-axis and even numbers are on the y-axis. This formation will relax your difficulty a lot. In this case, your formula y=1/2x has to be changed as y=2x. OK?

Noureddine Mohiti, Have you deleted my comment here?

NM: Age Baba I didn’t delete any comments

MN: Noureddine Mohiti, Never mind. Perhaps I myself mistakenly deleted or closed my browser unconsciously before I posted it. Anyway I found that even with my scenario to draw your graph is not easy because your vertex is not a number but a map. I cannot find any mapping from a map to other maps.

Now the session closed for today. You have to work on your own task. It’s your homework tonight.

NM: Thank you Master

MN: OK. As your homework seems to be unfinished and delayed I’ll give you a little more time. But this may be the last chance for you to pass the examination.

Let’s keep going.

I want to introduce a bit more complicated version of our bipartite Collatz graph as we know that we have to add a bit more lines on the graph anyway.

Here it is! This is the detailed version of bipartite Collatz graph. Hereafter we call this graph as Collatz B-graph.

We added red lines downward to the right on the graph. A red line represents a Collatz map like 2^c * n → n, where c is a natural number and n is odd.

The most remarkable point of this graph is that the regularity in the original B-graph is still kept firmly although it seems that some irregularity is observed near the left side line. But it’s untrue. These are mainly mapping from 2^c to 1. Odd numbers must have parallel lines with same slopes but we will examine these lines later.

Geometrical observation

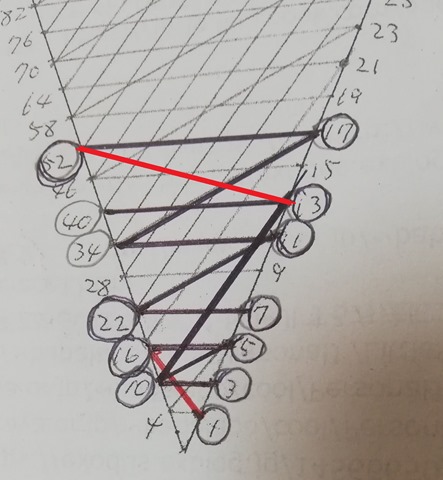
We successfully confirmed that layer 2 vertices are connected to layer 1.

Open Sesame! And the first door was opened toward the goal of mathematical induction. Let’s move on to the next step.

NM: Yes let’s go

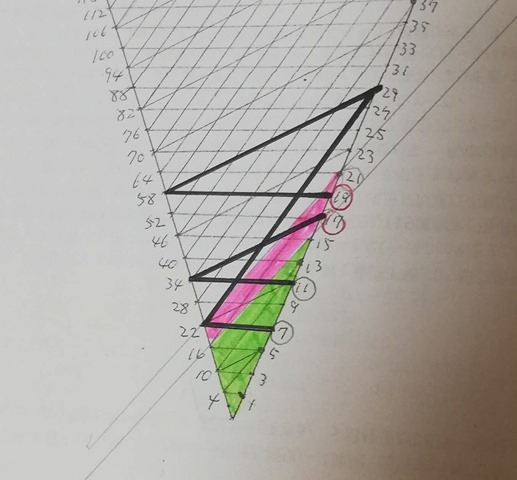
MN: This is the layer 3 challenge. Can you solve this?

This time your task is to connect 4 odd numbers {29, 31, 35, 37} to layer 2 + layer 1 vertices. If this assignment is easily accomplishable then we are almost done.

NM: I see something like graph theory (the numbers are vertex). If we prove that graph can reach to any vertex must be proven

MN: This is of course an application of exact graph theory but as you see our intention is to apply geometrical observation on it. Because we have to find out some pattern in chaotic movement of the orbits in ordinary Collatz graphs.

Solved but not so straightforward.

Are there any pattern or rule in this formation? Anyway we need a bit more experiment. I’m going to test layer 4.

Here comes layer 4. Surely it is SOLVABLE in anyway.

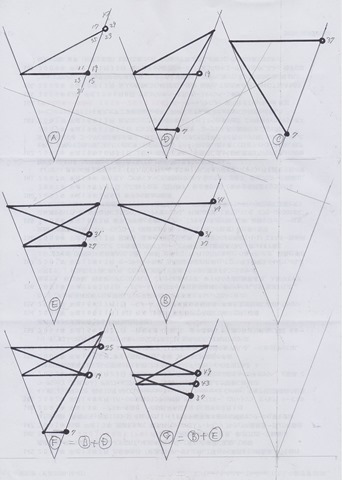
I’ve found 7 patterns in this graph.

A path (connection route) starts at a white circle point and ends at a black point.

Among them 2 patterns seem to be a composite of more primitive patterns, i.e. [F]=[B]+[D] and [G]= [B]+[E]. I suppose, this means that our formation was a bit excessed. There is no reason to let a layer have two even numbers. Perhaps it is simply Ok like one layer one even number formation.

The Collatz Compass graph

Before proceeding further I want to draw a full bipartite version of B-graph (bipartite Collatz graph). Here a full bipartite means that the diagram is drawn in a sense of the original definition of bipartite graph.

In graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets U and V such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

In this graph all of the horizontal lines are abbreviated to make the graph more easily readable. This graph is absolutely equivalent to our B-graph in the sense of graph theory. The difference among the two graphs is just the distance in the display between vertex 4 and vertex 1 merely on the appearance.

The characteristics of the full version bipartite Collatz graph is that every edges in the graph has different slope except the horizontal lines, i.e. there are no parallel lines in it except horizontal lines. It will make so hard or impossible to analyze the total connection among odd vertices.

I just have conceived a slight question in the description above saying that a bipartite graph is a graph that does not contain any odd-length cycles. I believe that 3n-1 version Collatz graph can be drawn in the same way of our Collatz B-graph, i.e. drawable as a bipartite graph. However we know that 3n-1 version Collatz graph has an odd hole length 5. What’s that?

It is simply true that a bipartite graph has no odd cycles as it is essentially impossible. The odd cycle in 3n-1 version Collatz is the cycle(5, 14, 7, 20, 10) and it contains an edge(20, 10). This is an edge even to even. That’s it. In our B-graph there is no such an edge between two even numbers. In other words 3n-1 version Collatz B-graph has an even cycle length 4.

Now we found out that the most significant factor of our solution comes from the “appearance” of the Collatz B-graph. Although this graph is bipartite and has two side lines (parts) at the left and right side these lines must be not parallel but crossing at the origin zero point like a compass. Hence hereafter we call this graph as Collatz Compass Graph.

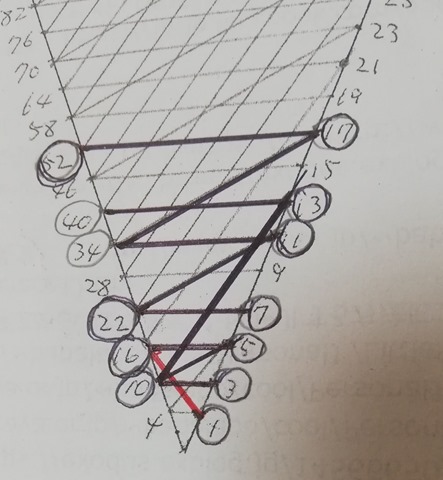
Let’s continue our experiment. This time I’m going to test one layer one even number method for a mathematical induction step. Assume that we already know that every number under 16 has an undirected path to 1. We call the set of vertices under 16 as layer 1. Layer 2 consists of a set of 4 vertices {22, 17, 19, 21}.

As always we neglect vertex 21 as it is a multiple of 3.

Vertex 17 goes to 11 using pattern [A] above and vertex 19 goes to 7 using pattern [D].

Layer 3 using [A] and [E] pattern

Layer 4 using [A] and [C]

Layer 5 using [A] and [G]

Layer 6 using [A] and [B]

What can I say with these results?

Clearly pattern [A] is applicable for every layer. This is of course a good news. This means 1/3 of odd numbers are easily connected to the lower layer. We already neglected 1/3 of odd numbers because of the reason as multiple of 3. Therefore we can concentrate other 1/3 of odd numbers. This is a pretty good start. Patten [A] is a 2-path like n→n/2→(n/2-1)/3 and n=6m-1 : m is a natural number.

As well pattern [B] is a 2-path like n→3n+1→(3n+1)/2 and n=8m+1: m is a natural number. How about pattern [C]? This is a 2-path like n→3n+1→(3n+1)/2^c. Therefore [B] is considered to be a special type of [C] such as c=1. I’m not sure how is the distribution of the number of this type. Supposedly excepting c=1 case, it seems that such numbers are pretty sparse.

Every pattern can be decomposed to one or more 2-paths. And perhaps we also had better consider to go in reverse direction, i.e. upward movement. We have to marshal all elements a bit more clearly and get them straight. Surely this is the toughest and most challenging task.

Every odd number n such as a multiple of 3 is a leaf on any contracted Collatz tree

Now that your submission deadline has already expired I’ll show you the answer for your assignment:

Proposition: Let odd number n be a multiple of 3. Then there is no trajectory (a sequence of Collatz mapping) from any other odd numbers to the number n.

Proof: Let odd number n=3m where m is an arbitrary odd number. From the definition of Collatz graph we have an infinite even number sequence S like {2n, 4n, …, n*2^c, … ∞} connected to the node n. Assume that the proposition is false then there must be an even number Y in the number sequence S such as Y=n*2^c and Y=3X+1 where X is an odd number. Then we have an equation:

n*2^c = 3m*2^c = 3X+1

m = (X+1/3)/2^c

Apparently there is no such integer m. Thus the assumption does not hold. QED

Every number with value 3m i.e. a multiple of 3 is a leaf in any contracted Collatz tree. It means that the distance from number 3m to 1 is relatively larger than other nodes on the trajectory. In other words starting from a 3m node is the toughest way to seek the trajectory while we can avoid such difficulty due to this theorem.

You can say that given any Rubik pattern is solvable even if you don’t know how to do it

We acknowledged that even with our superior Collatz Compass method it seems that our goal is still far far away. What shall we do or what can we do? Now I want to give you a similar situation. Can you solve a Rubik’s cube? Can you solve any patterns of the cube? Is there any complete method known to solve all Rubik’s patterns. Are there any patterns known to be impossible to be solved? I don’t know. But you can definitely say that given any pattern is eventually solvable in anyway even if you don’t know how to do it.

Why? That is, you know that any patterns were made from the first starting face set within a finite manipulation. So the reverse procedure must be always possible. I think that this reasoning is applicable for our case, that is, even if we don’t know an actual trajectory for some node, we can say that the trajectory goes down to number 1 eventually. We will call this methodology as the Rubik Reverse Tracking.

NM: It solved by group theory

MN: Please show me!
Sorry, you meant about Rubik’s cube.
Are there any distributions of colors in faces impossible to be solved?

NM: Age Baba, the solution came from group theory

MN: Thanks.

NM: Age Baba, yes there are some videos in YouTube. Explain the methods of solution

MN: Are there any distributions of colors in faces impossible to be made by hand?

NM: I’m a bit busy , with cymatics

MN: Noureddine Mohiti, Interesting!

Formulation of the Collatz compass graph

MN: I augmented the Collatz Tree diagram showing the orbits of the odd numbers less than 50 by adding lacking nodes and more in it. How can we applicate the Rubik reverse method on it? I’m not sure but I tried to supplement even numbers (red color, in Collatz Compass graph they are allocated on the left side line) between each adjacent two odd nodes pair (in other words on each edge).

This handwork gave me a great insight that every edge connecting two odd nodes in the Collatz Tree appeared to be a 2-path like hook shaped in the Collatz Compass graph. This is not so surprising discovery but I suppose it would make our task much easier.

I didn’t use a calculator so I might mistook somewhere…

Very sorry! As I expected I had made a big mistake in the tree. I have to redraw it but maybe later…

In the Collatz Compass graph there are 6 types of lines. One is horizontal (n→3n+1), two are ascending (rising to the right, n→2n, n→(3n+1)/4) and three are descending (downward to the right, n→4n, n→16n, n→n*2^c ). Every 2-path connecting adjacent two odd nodes in Collatz Tree is consist of a horizontal line and a slope line in the Collatz Compass graph. So they look like a hook.

Perhaps we no more need to use complicated composite paths like pattern [F] or [G].

We can consider that two lines n→4n and n→16n are a kind of n→n*2^c line but n→2n line is a bit different because this line is ascending while n→n*2^c lines are descending.

Correction: in this picture,
Incorrect: 16n
Correct: 8n

Let’s go on. I suppose that the Rubik reverse method is a quite promising approach because if we can apply this method then we’ll be able to say every node n eventually goes to 1 without actually showing the trajectory.

Furthermore we found out that an edge in contracted Collatz tree corresponds to a 2-path in Collatz Compass graph. It is sure that an edge connecting two odd numbers v(m) and v(n) in the Collatz tree must be a round trip like odd number R(m) → even number L(3m+1) → odd number R(n) where L and R are the two parts of Collatz Cross bipartite graph.

But here exists a slight problem. Some node (odd number) pair m and n may have plural of 2-paths. For example edge(69, 13) has two 2-paths like {69, 52, 13} and {69, 208, 13}. As well edge(53, 5) has 2-paths {53, 160, 5} and {53, 46, 5}. What should we think this?

I think that a 2-path including a horizontal line is much more normal than the other. If this is true then we might able to eliminate all the ascending lines n→(3n+1)/4 from the Compass graph. I’m going to rewrite the compass graph like that. We will have a bunch of descending lines with various slopes like 4n, 8n, …, n*2^c and one ascending line with a slope 2n.

I rewrote the Collatz compass graph eliminating ascending lines n→(3n+1)/4 and adding descending lines n→16n. I think the compass graph is ready to use.

Now we are ready to formulate the compass graph.

The compass graph G is an undirected bipartite graph
G has two parts (vertex set) R and L
R is an infinite set of odd numbers {1, 3, 5, … 2x+1, … ∞} : x is an integer from 0 to ∞
L is an infinite set of even numbers {4, 10, 16, … 3y+1, … ∞} : y is an integer from 1 to ∞
Every node n in R joins to the node 3n+1 in L
Every node m in L joins to the node n in R where m=n*2^c : c is an integer from 1 to ∞
Hence every even node m in L has two edges
If an odd node n in R is a multiple of 3 then it has only one edge e(n, 3n+1)
Otherwise n has infinite number of edges like e(n, n*2^c) : c is an integer from 1 to ∞

Surely this formation is nothing but the definition of Collatz sequence. Are there any good things here? All we need to do is to prove the connectivity of the graph. I believe that it is no brainer. But how?

Anyway I’ll try to make this graph a bit simpler. As I said above at the clause 8 if node n is a multiple of 3 then it has only one edge. This means that any multiple of 3 node n has no relevance with the connectivity. So we can eliminate those vertices from the graph.

NM: I will send you my last vision of Collatz conjecture

MN: Please!

I think that to purge all multiple of 3 nodes is not so bad idea but the result was miserably beyond my imagination. It just revealed that the problem is really very hard. What can I do?

Black, red and blue lines are all connected to 1 but other lines are still disconnected. How can I do?

The only good thing is that we confirmed purging multiple of 3 numbers never effects on the connectivity.

I wrote a simple VB code for you to dump a Collatz mapping list.

Private Sub Button1_Click(sender As Object, e As EventArgs) Handles  Button1.Click
    Dim MAX As Integer = Val(MaxNumber.Text)
    Dim i As Integer = 0
    For i = 0 To MAX / 2
        Dim odd As Integer = i * 2 + 1
        Dim even As Integer = odd * 3 + 1
        Dim odd2 As Integer = even
        Do While CInt(odd2 Mod 2) = 0
            odd2 = odd2 / 2
        Loop
        Console.WriteLine("{0}. {1} {2} {3}", i + 1, odd, even, odd2)
    Next
End Sub

Here is the sample output for the first 50 odd numbers.

Line format #. x y z x:odd y:3x+1 z:y=z*2^c

1 4 1
3 10 5
5 16 1
7 22 11
9 28 7
11 34 17
13 40 5
15 46 23
17 52 13
19 58 29
21 64 1
23 70 35
25 76 19
27 82 41
29 88 11
31 94 47
33 100 25
35 106 53
37 112 7
39 118 59
41 124 31
43 130 65
45 136 17
47 142 71
49 148 37
51 154 77
53 160 5
55 166 83
57 172 43
59 178 89
61 184 23
63 190 95
65 196 49
67 202 101
69 208 13
71 214 107
73 220 55
75 226 113
77 232 29
79 238 119
81 244 61
83 250 125
85 256 1
87 262 131
89 268 67
91 274 137
93 280 35
95 286 143
97 292 73
99 298 149

I’ll show you later the result drawn in a tree format.

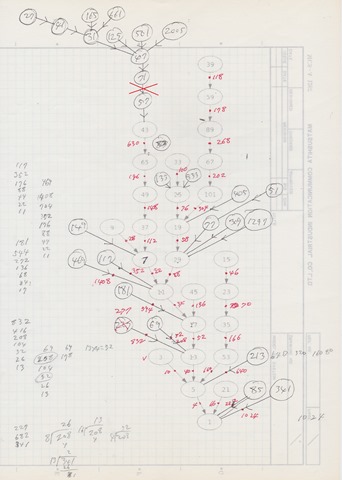
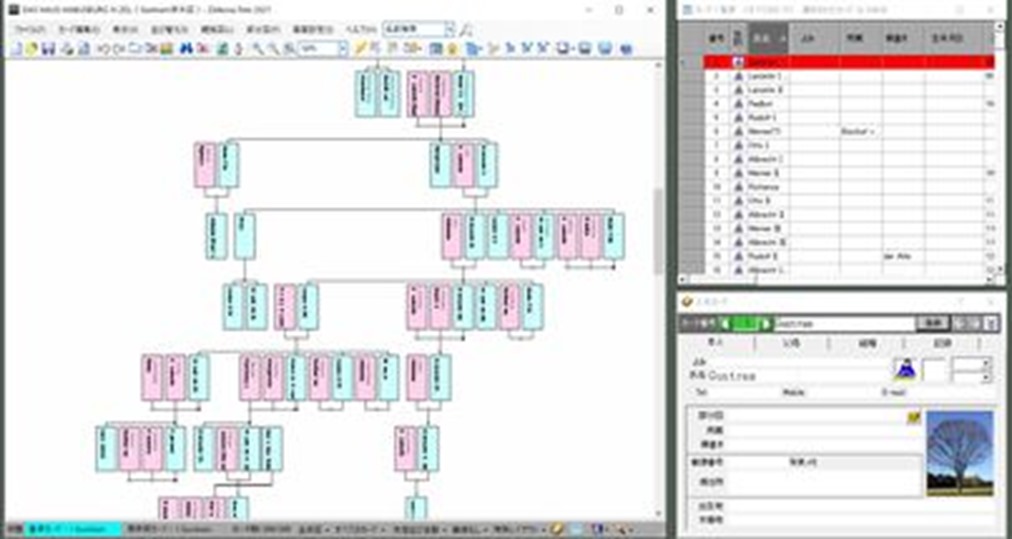
Our Zelkova Tree genealogy builder is able to draw Collatz tree

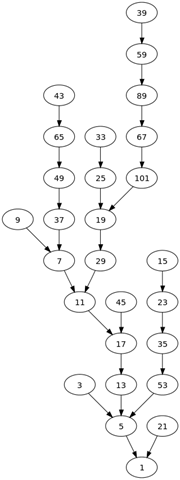
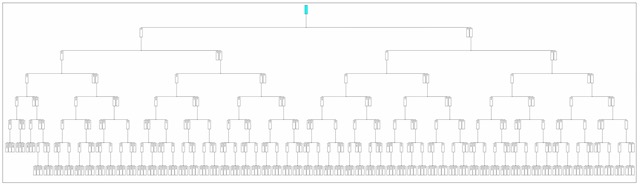
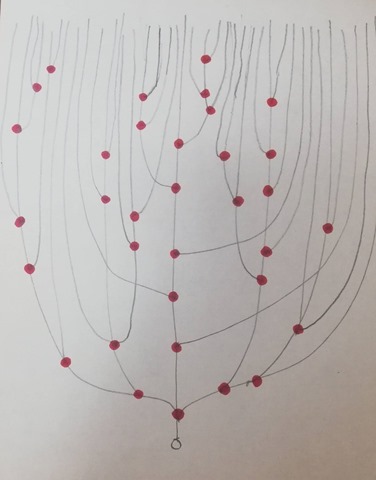
Collatz Tree under 99 built by Zelkova Tree

Genealogy builder Zelkova Tree is our product (Baba Laboratory). Admittedly it is the incomparable and ultimate genealogy software in the world.

Example: Hapsburgs family tree on Zelkova Tree

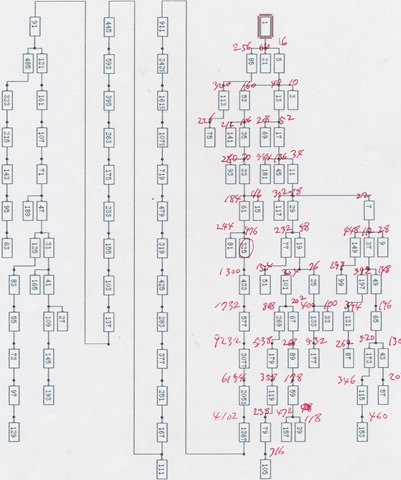
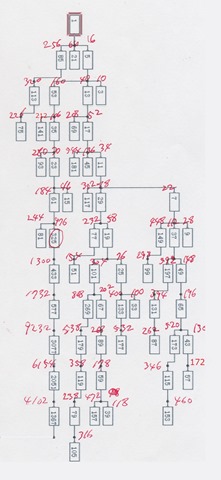
Collatz Tree under 121 built by Zelkova Tree [necessary some additional handwork with a painting tool]

This is a 120 nodes tree and contains continuous odd numbers up to 121.

Those very young numbers like 27, 31 and 41 are near the tail of the chain.

The maximum odd number in this tree is 3077.

A boy and a girl may have “relation” or may have not

Today I want to talk about friendship. What’s a friend? Suppose that there are numerous boys and girls in a room. A boy and a girl may have “relation” or may have not. Boys have no “relation” among them as well as among girls. We define friendship like this. If two people have a “relation” then they are friends and a friend of a person’s friend is a friend of the person. We can say that if A is a friend of B then B is a friend of A and if A is a friend of B and B is a friend of C then A is a friend of C. We trivially suppose that A is a friend of A.

In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. Apparently friendship is an equivalence relation and we know that an equivalence relation splits the set S to a plural of disjoint equivalence class. Hence our concern is like are there any partition boards in the room completely separating them into different companions. [If not then the Collatz conjecture is true… ]

We consider the reduced version Collatz compass graph with no odd number k of multiple of 3 and the even number 3k+1 (k’s partner). In this graph each girl (even number) has relation with two boys (odd number) but any boys are allowed to have any number of “relations” with girls. But any two boys do not share a girl while a girl shares a boy with other girls. Answer this question: Do you need a partition board in the room or not?

Sorry. The description above is incorrect. Some two boys share a girl.

How to certificate the delivery route of chain letters?

Have you ever received a chain-letter? A chain letter is a message that attempts to convince the recipient to make a number of copies and pass them on to a certain number of recipients. The “chain” is an exponentially growing pyramid (a tree graph) that cannot be sustained indefinitely. There are two kinds of chain letters, one is called fortune letters and the other unfortune letters.

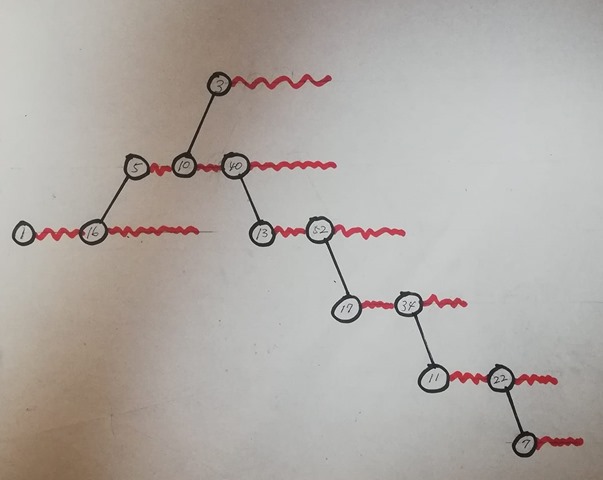
I don’t like neither of them but I came up with an idea to use it for solving Collatz problem. The procedure is simple. The first message is sent from node(1) with its signature “1” at the bottom line to every neighbors of it. The message must be transferred to the neighbors of the recipient adding its signature at the bottom line. A sample of signature list would be like {1, 16, 5, 40, 13, 52, 17, 136, 45}. Given an odd number n and you can make the signature list which starts from 1 and ends at n like {1, …, n}. Don’t you think that such a signature list would be acceptable as the certification that node(n) is really connected to node(1)?

NM: I am still working on the binary formula of Collatz conjecture it is so beautiful but so sinking.

MN: Noureddine Mohiti, Good!

OK. There exists a much straightforward way to prove Collatz conjecture just draw the Collatz tree bottom up in the manner of the compass graph.

LOOOK! I was able to do it! I’m very sorry for all of you. Because our solution is incredibly simple and elementary!!!! ⛳️

I found two mistakes on the tree and replaced it.

The tree above tells us all.

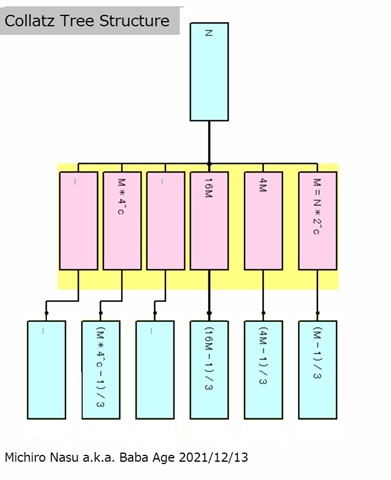
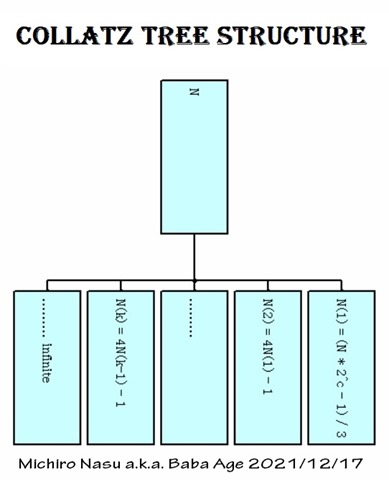
This diagram explains how to build the complete Collatz tree in bottom up way starting from node 1.

In this diagram odd numbers are painted blue and even numbers are painted pink. An arbitrary odd number n has an infinite number of even numbers M(i)=M*4^i : i=0 to ∞ in the cell (yellow box). M is the right most even number in the cell like M=N*2^c : c=1|2|3|4. Every even number m has one and only one odd number (m-1)/3. That’s all.

Every odd number n has an infinite subtree except a multiple of 3. We’ve got the complete Collatz tree structure. Finally Collatz Problem has been solved.

To avoid a possible confusion I erased the yellow colored frame around odd numbers and replaced the picture.

I believe you can supplement this idea and write down a complete proof.

Collatz tree is a fractal !!

Collatz tree is a fractal, is this true? I bet so. Because every part of the tree is built out of a simple Collatz Tree Structure shown above. Mandelbrot says “A fractal is a shape made of parts similar to the whole in some way.”. I’ll show you later a whole figure of Collatz tree.

Every fractal has its own fractal dimension. Can you calculate the dimension of a Collatz tree?

Here it is! Collatz Tree is a fractal.

To get your Collatz Black Hole image easily you had better use cone-shaped dropping downward spiral lines instead of this plain spiral. I request you to draw a picture more realistic and like fractal one.

In this picture a spiral line corresponds to a yellow box (a set of even number M*4^c) on the Collatz Tree Structure above. A red line corresponds to the Collatz mapping such as odd number N to even number 3N+1.

How about this? Do you like it? If you do I’ll give you this picture as a reward for your contribution all through this steep and turbulent process.

You can auction this picture as a digital art with NFT (Non-fungible token) on the net. Indeed lastly Winkelmann, aka the digital artist Beeple, has sold his digital art and earned $69 million.

Now you may understand clearly why I did say that we need N pieces of wire to knit a Collatz basket. N equals to the number of odd numbers in the basket. If you have a skill to knit metal wires into a basket it’s easy for you to make a Collatz basket out of Collatz Black Hole wire model above.

I said in my earlier comment “I think my graph is essentially equivalent with yours if I understand you correctly”. I want to know whether this tree is what you’ve expected or not?

You may think that this graph is wrong because joint points must be upper than spiral ends as 3n+1 > n. Yes, you are right in a way but not wholly. This graph is meant to show the graph topology but not for accurate spatial placement. In fact even if you move spiral A downward as below the graph topology doesn’t change at all. OK?

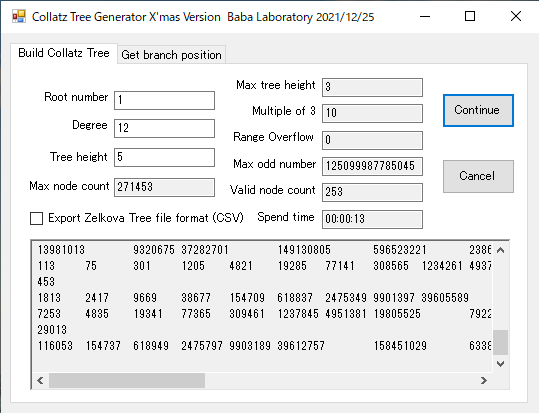
To build a regular Collatz tree generator

Currently I’m working to write a program for outputting a 3-regular Collatz tree such as every odd node is adjacent to exactly 3 even nodes. This is a pretty tough job. The growth of the number of nodes is exponential (a tree of only height 8 has 9841 nodes) and to make matters worse the number value becomes too large and easily causes integer range overflow (> 2147483647)… How can I do?

Sorry. Accurately this graph is not a 3-regular. Even if the graph contains only odd nodes it should be rather called as 4-regular because we need one more edge for connecting to the upper node.

There are confusions even in literatures. At the first if we define regular tree such that a regular tree is a tree in which every vertex has the same degree then we have only K1, K2 or infinite trees. Accordingly the most usual definition of regular tree is like this. A regular tree is a tree in which every vertex that is not a leaf has the same degree. However sometimes it is said like a binary tree is 2-regular (actually this is 3-regular on the previous definition). We’ll talk about this later but I believe that you understand what I intended to say using “3-regular” here. Yes, I meant “trinary tree”.

I wrote a small program to output the node number list of an arbitrary Collatz k-regular tree in console. This program is both time and space consuming. In the case of 4-regular tree (trinary tree) we could only get the list of at most tree height 14 (very short). This tree has virtually 7174453+1 nodes. As far as I remember I got the result in 1 hour or so but today It is running still after 2 and a half hours… I might better restart my PC. Beforehand the number 7174453 is a bit strange. As this tree is trinary the number must be a multiple of 3…

No, my misunderstanding. The number 7174453 includes 1 in advance. The number 7174453-1=7174452 is devisable by 3. Perhaps the condition for yesterday’s test was much lighter than today. I don’t remember well but I suppose it was under the condition of excluding numbers larger than 100000. Today I’m testing all the numbers except numbers out of the range of integer. So the current test is said to be the most authentic.

It’s still running after 4 hours at about order 4980000. Yesterday’s test outputted 6808695 odd numbers. So we still have 1 million nodes to be processed… The dump data outputted are being erased from the console screen as time going. The test is almost halted at the number 4981667. Using CPU ratio is 6-7% and using memory ratio is 35%. I think that the amount of usable memory for the application is perhaps over its limitation allowed. It is of no use to continue this test furthermore…

After I rebooted the OS it ran quite well and soon finished the test. I want to count the number of omitted over range numbers and numbers of multiple of 3 as well as total number of valid nodes.

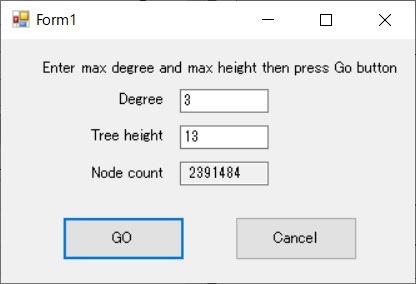
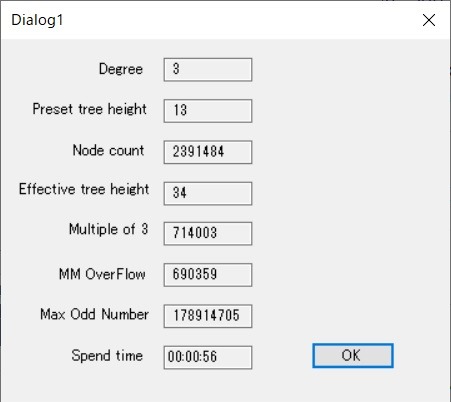
I almost finished my debugging of the program. Good enough. Time efficiency is not so bad as I thought. Time consuming part is mainly dumping of the result onto the console. For the case of the tree with setting degree 3 and height 13 it takes less than 1 minute to calculate 2391484 nodes.

Node count is automatically calculated when “degree” or “height” is changed. It might be a bit confusing to use “degree” here. I meant k-ary by k-degree.

The tree height 13 means a very short tree but the involved numbers are not at all small. The largest odd number in this tree is 178914705 but actually overflows are happening at as much as 690359 places.

The preset tree height and the actually generated tree height (effective tree height) usually differ because a lot of x3 nodes and integer range overflow would happen at many places. It makes the tree much sparse and remaining reserved nodes are allocated to make the tree further taller.

In this case the preset tree height is 13 but the result is a height 34 tree. The tree grows by 11 in height.

Here is the first 20 lines and the last 20 lines of the dump list. Line format is like:

#: odd number N: { M=3N+1→N(i)=(M-1)*2^c } i=1…[degree]

“x3” stands for an odd number such as multiple of 3. “MM OVER FLOW” means an overflow happened when calculating M*4^c where M is the right most even number in the cell (yellow box shown before).

0: 1: 16→5　64→21　256→85
1: 5: 10→3　40→13　160→53
2: 21: x3
3: 85: 340→113　1360→453　5440→1813
4: 3: x3
5: 13: 52→17　208→69　832→277
6: 53: 106→35　424→141　1696→565
7: 113: 226→75　904→301　3616→1205
8: 453: x3
9: 1813: 7252→2417　29008→9669　116032→38677
10: 17: 34→11　136→45　544→181
11: 69: x3
12: 277: 1108→369　4432→1477　17728→5909
13: 35: 70→23　280→93　1120→373
14: 141: x3
15: 565: 2260→753　9040→3013　36160→12053
16: 75: x3
17: 301: 1204→401　4816→1605　19264→6421
18: 1205: 2410→803　9640→3213　38560→12853
19: 2417: 4834→1611　19336→6445　77344→25781
20: 9669: x3
————————————————-
2140743: 45188061: x3
2140744: 90376129: 361504516→120501505　1446018064→482006021　i=0 j=1 MM OVER FLOW 1446018064
2140745: 22594043: 45188086→15062695　180752344→60250781　723009376→241003125
2140746: 90376173: x3
2140747: 45188087: 90376174→30125391　361504696→120501565　1446018784→482006261
2140748: 22594055: 45188110→15062703　180752440→60250813　723009760→241003253
2140749: 90376221: x3
2140750: 45188111: 90376222→30125407　361504888→120501629　1446019552→482006517
2140751: 90376225: 361504900→120501633　1446019600→482006533　i=0 j=1 MM OVER FLOW 1446019600
2140752: 22594247: 45188494→15062831　180753976→60251325　723015904→241005301
2140753: 90376989: x3
2140754: 45188495: 90376990→30125663　361507960→120502653　1446031840→482010613
2140755: 90376993: 361507972→120502657　1446031888→482010629　i=0 j=1 MM OVER FLOW 1446031888
2140756: 353031: x3
2140757: 1412125: 5648500→1882833　22594000→7531333　90376000→30125333
2140758: 5648501: 11297002→3765667　45188008→15062669　180752032→60250677
2140759: 11297009: 22594018→7531339　90376072→30125357　361504288→120501429
2140760: 45188037: x3
2140761: 90376113: x3
2140762: 706063: 2824252→941417　WX > MAX WX=2391484 MAX=2391484

The explanation above about the line format is somewhat wrong. Correctly:

Line format is like:

#: odd number N: { M(i)→N(i)=(M(i)-1)/3 }
M(1) = 3N+1 and M(i)=4*M(i) for i>1 : i=1…[degree] :

“x3” stands for an odd number such as multiple of 3. “MM OVER FLOW” means an overflow happened when calculating M*4^c where M is the right most even number in the cell (yellow box shown before) where c is an integer {0, … ∞}.

I’m going to try to draw a 3-regular (trinary) Collatz tree using our Zelkova Tree genealogy builder. Zelkova tree can only draw a tree with at most 1000 nodes. So degree 5 or 6 are the upper bounds. Degree 5 generates 364 nodes tree and degree 6 outputs 1093 nodes. Let’s try!

3-regular (trinary) Collatz Tree 364 points built by Zelkova Tree

NM: Thank you Sir . I just busy with confused work in physics and zeta function my brain are blowing

MN: OK. If you like I can send you a copy of original PDF file. The picture above is too bad to read numbers but they are clearly readable on the PDF file.

NM: Age Baba, yes sir.

MN: I just sent you a copy. Enjoy!

I’ve just uploaded the PDF to the file archive of this group. Anybody in this group is able to download.

Can you believe this?

This is the secret of Collatz Tree revealed.

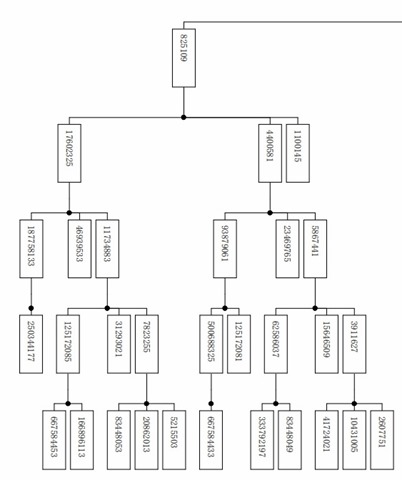
Let N be an odd number on Collatz Tree and N(1) be the 1st successor of N then k-th successor N(k) = N(1) * 4^(k-1) – 1. That’s all.

To give a proof is your turn.

Collatz conjecture is a problem of which question can be understood by an elementary schoolboy and also/therefore the answer is as easy as an elemental schoolboy is able to understand.

I’ve just uploaded Collatz Tree 1000.PDF to the file archive of this group. Anybody in this group is able to download. This tree includes 1000 odd numbers. Among them the largest number is 667584453. The tree height is 9 (10 generations).

Any PDF viewer has a rotate tool (button). Zoom in to 500% and rotate the Tree 90/270 degree then you can read the numbers much easily.

Like this!

Regretfully Acrobat Reader (free version) doesn’t have the rotate function. To subscribe Acrobat Pro DC costs $15/month but you may use the trial version for free for 7 days. [The merit to use Acrobat Reader is its search function.]

This is a part of the tree at the left and bottom corner. You’ll find the largest number 667584453 here.

Let’s take a break

I made a Collatz spiral wire as a trial by hand but not so much good…

Please make more realistic one (much cone shape like) by yourself.

NM: I find a methods to do cymatics by electromagnetic waves. Some physical phenomenon are generator of mathematics logic. Specially dimension

MN: Noureddine Mohiti, Are you going to disclose your method to the public? Or do you want to be an African magician?

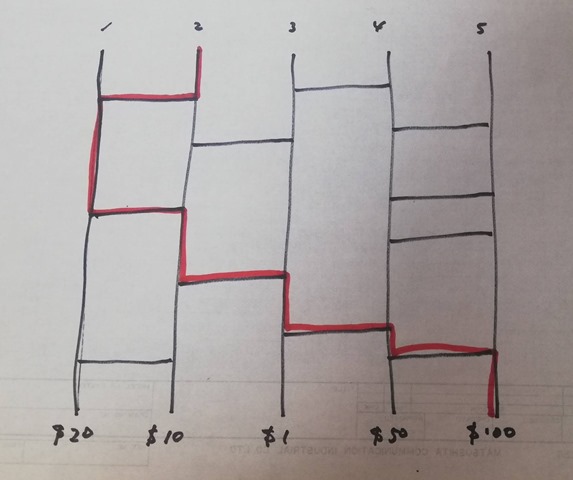
It’s amusing to play an amida-kuji game that’s a kind of lottery known as Japan origin. You need only a sheet of paper and a pencil to play with. The rule is simple. At first you draw N vertical lines for N participants and add several horizontal lines between two vertical lines neighboring. Select a line and go downward. When you encounter an intersection then you have to turn horizontally and go on.

To make the game much difficult any participants are allowed to add horizontal lines as they like. In this game every entry point has a different goal, that is, any two persons don’t encounter at the same goal. This is a fact. Can you prove it graph-theoretically? Have fun!

One more question. It seems that for every vertical line segment (vertical edge) just one person goes through it and every horizontal line segment (horizontal edge) is shared by two persons without exception. In other words every vertical line is traced just once and every horizontal line is traced exactly twice. Right? Then you are asked to prove it. Good luck!

Merry X’mas and a happy new year to all. This is another expression of the Congratulations Collatz Tree.

Final answer for the Collatz conjecture

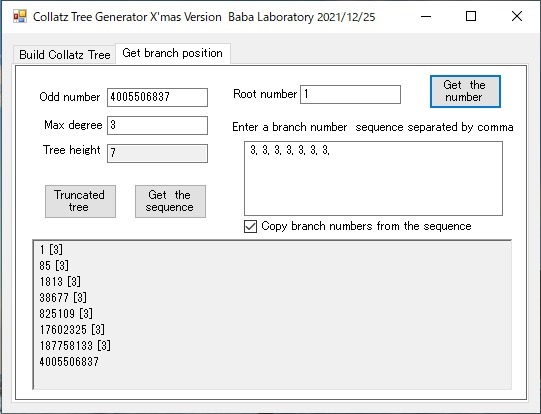
I want to write a program which outputs the position of any odd number N like (d, h, b, l) in a regular Collatz tree where d is the degree (d-ary) of the tree, h is the height (generation) of N, b ≤ d^(h-1) is the branch order from the right most branch in the second lowest layer of the tree and l ≤ d is the leaf order in the branch.

Done! Here comes Collatz Tree Generator.

With this tiny tool you can generate any size of Collatz tree (within the ULong integer range ≤ 18446744073709551615 = 2^64 – 1) and seek the branch position of any odd node in the tree. Try it! [The screen layout changed in the final version.]

The output format is a tab-separated adjacency list in which a line is like:

N n_1 n_2 n_3 … n_d : d is the “degree” you designated.

N is an odd number and n_1, n_2, … are its child nodes. That is, there are edges N→n_1, N→n_2,…, N→n_d in the tree. You can copy and paste this list to your spread sheet or any other graph tool.

Branch position tool outputs a Collatz number sequence for an designated odd number like:

N
n_1[2]
n_2[1]
:
n_i[k]
:
1[1]

N is the odd number and { n_1, n_2,…, 1 } is the Collatz sequence as you are familiar with. n_i[k] means that the successor n_(i-1) of n_i is placed at the k-th branch of node n_i .

Do you think that we’ve solved the problem?

If you like I’m willing to upload the whole package including the full source code written in Visual Basic into the archive of this group.

Furthermore you can output any subtree of Collatz Tree by designating any odd number as the root of the subtree.

I want to add one more function to our program. You can input a sequence of branch position like {2, 1, 3, 1, 5, 2, 4} then the tool answers the odd number at the position at once. Don’t you think that it’s a kind of magic? It will be a perfect realization of your “reverse method”. [ Or it is said to be a kind of realization of the chain letter certification. ]

Completed! What? Collatz Tree Generator.

This is our final answer for the problem.

I wanted to share this program with anyone who is interested in Collatz Problem, but unfortunately executable files are prohibited in the group feature. If you have an interest in this tiny tool, please send me a message and tell me your e-mail address. I’ll send you back soon. I need your help.

You can download this program (CollatzTreeGenerator.exe 41984B) for free from here. Published 2022/01/03 M.N. Baba Laboratory babalabos@outlook.jp